Gödel, Escher, Bach by Hofstadter
Ref: Douglas Hofstadter (1979). Gödel, Escher, Bach: an Eternal Golden Braid. Basic Books Inc.
___________________________________________________________________________
Summary
GEB is a very personal attempt to say how it is that animate beings can come out of inanimate matter…GEB approaches these questions by slowly building up an analogy that likens animate molecules to meaningless symbols, and further likens selves (or “I”s or “souls”, if you prefer- whatever it is that distinguishes animate from inanimate matter) to certain special swirly, twisty, vortex-like, and meaningful patterns that arise only in particular types of systems of meaningless symbols…I call such strange, loopy patters “strange loops” throughout the book, although in later chapters, I also use the phrase “tangled hierarchies.”
Do words and thoughts follow formal rules, or do they not? That problem is the problem of this book.
GEB is, in essence, a long proposal of strange loops as a metaphor for how selfhood originates.
One of the main theses of this book is that every aspect of thinking can be viewed as a high-level description of a system which, on a low level, is governed by simple, even formal, rules. The "system" , of course, is a brain.
Tangled Hierarchy: A system in which a strange loop occurs.
Strange Loops: A phenomenon that occurs whenever, by moving upwards (or downwards) through the levels of some hierarchical system, we unexpectedly find ourselves right back where we started.
Gödel’s Incompleteness Theorem (1931): In any reasonable mathematics system, there will always be true statements that cannot be proved.
We can liken real-world thought processes to a tree whose visible part stands sturdily above ground but depends vitally on its invisible roots which extend way below ground, giving it stability and nourishment. In this case the roots symbolize complex processes which take place below the conscious level of the mind-processes whose effects permeate the way we think but of which we are unaware…According to my hypothesis, imagery and analogical thought processes intrinsically require several layers of substrate and are therefore intrinsically non-skimmable. I believe furthermore that it is precisely at this same point that creativity starts to emerge- which would imply that creativity intrinsically depends upon certain kinds of “uninterpretable” lower-level events.
AI Thesis: As the intelligence of machines evolves, its underlying mechanisms will gradually converge to the mechanisms underlying human intelligence.
A central issue of this book is: "Do words and thoughts follow formal rules?" One major thrust of the book has been to point out the many- leveledness of the mind/brain, and I have tried to show why the ultimate answer to the question is, "Yes—provided that you go down to the lowest level- the hardware- to find the rules."
The point of this book has been to show, how in any system there is always some "protected" level which is unassailable by the rules on other levels, no matter how tangled their interaction may be among themselves.
My belief is that the explanations of "emergent" phenomena in our brains- for instance, ideas, hopes, images, analogies, and finally consciousness and free will- are based on a kind of Strange Loop, an interaction between levels in which the top level reaches back down towards the bottom level and influences it, while at the same time being itself determined by the bottom level. In other words, a self-reinforcing "resonance" between different levels-quite like the Henkin sentence which, by merely asserting its own provability, actually becomes provable. The self comes into being at the moment it has the power to reflect itself.
What we consider to be conscious arises from a tangled hierarchy of systems, meta-systems, meta-meta systems, meta-meta-meta systems and so on, all working in tandem through a series of strange loops (Me).
___________________________________________________________________________
Preface
The Gödelian strange loop that arises in formal systems in math is a loop that allows such a system to “perceive itself”, to talk about itself, to become “self-aware.”
Russell believed that for a mathematical system to be able to talk about itself in any way whatsoever was the kiss of death, for self-reference would, so he thought, necessarily open the door to self-contradiction, and thereby send all of mathematics crashing to the ground.
Gödel showed how a statement about any mathematical formal system (such as the assertion that Principa Mathematica is contradiction free) can be translated into a mathematical statement inside number theory.
By means of Gödel’s mapping, any formal system designed to spew forth truths about “mere” numbers would also wind-up spewing forth truths- inadvertently but inexorably- about its own properties, and would thereby become “self-aware.”
The twisted loop of selfhood trapped inside an inanimate bulb called a “brain” also has causal power- or, put another way, that a mere pattern called “I” can shove around inanimate particles in the brain no less than inanimate particles in the brain can shove around patterns. In short, an “I” comes about, in my view at least, via a kind of vortex whereby patterns in a brain mirror the brains mirroring of the world, and eventually mirror themselves, whereupon the vortex of “I” becomes a real, causal entity.
___________________________________________________________________________
---Part 1---
Part I is an exposition of many interesting and deeply related ideas: formal systems like math and physics acquire meaning by modeling the world; recursion gives these systems power but also enables self-reference; and self-reference ultimately poses a serious problem for these systems. These ideas build to the statement and proof of Gödel’s Incompleteness Theorem.
The basic object of study in GEB is what Hofstadter calls a formal system. A formal system consists of:
A collection of allowable characters out of which we can form strings (sequences of characters).
A collection of strings called "axioms”.
A collection of rules, or "inference rules," for changing some strings into others.
We imagine that the strings of our system are logical statements written in some formal language. And we imagine that the axioms are some logical statements that we assume to be true. So the "proof" is akin to starting from a known axiom and using the rules of logical inference to deduce some desired theorem.
tq system: t = times, q = equals, - = one, -- = two.
Hofstadter points out that jumping outside the system is an important feature of intelligence. Before I introduced the tq-system I told you what my intended interpretation was. But even had I not, it's very likely you would have discovered it after a few minutes writing down tq-theorems. Instead of mindlessly churning out an ever longer list of theorems, you would instead gradually notice the patterns, put down your pencil to think, and discover that you can predict what all the tq-theorems are without writing them down. These are all outside-the-system activities.
Contrast this with the behavior of a graphing calculator running a basic program that prints out a list of tq-theorems. The graphing calculator will never stop executing its code, step back to survey the data, notice the pattern, and print out IT'S THE MULTIPLICATIONS YOU DUMMY. Of course, a human is ultimately some program, albeit a very complicated one running on an extremely powerful computer. Accordingly, there is some system out of which we are unable to step, the same way biological evolution is unable to step back, take a look at the data, and shout into the void JUST KEEP MAKING MORE CRABS YOU DUMMY. The point isn't that human intelligence is "special" in some way that purely mechanistic reasoning can never replicate. The point is simpler: intelligent systems seem to be able to identify and run subtasks, as well as to monitor these subtasks from the outside and determine when to stop doing them.
Provability comes from a formal system and truth comes from the interpretation + context.
theorem" just means something you can deduce from the axioms using the inference rules, i.e. something you can "prove."
A formal system which is able to prove all of its truths is called "complete." So Gödel's theorem says that every sufficiently rich formal system is incomplete – there will always be unprovable truths. What does “sufficiently rich” mean? It means “expressive enough to permit certain types of self-reference”; more on that in the next section (i.e. P-- in the tqCP-system is true, but unprovable; P-- = 2 is prime).
Suppose that I were to walk into your room and say: “This sentence is a lie.” As I’m an untrusted stranger, you might suspect that I’m lying. But if that were the case, then "This sentence is a lie" would be the truth, so I’d be telling the truth ... a contradiction! Likewise, if you suppose I’m telling the truth, you'll come to find that I’m lying, another contradiction. (And at this point you should step out of your “solve logic puzzle” subtask and initiate a “report intruder to the police” subtask.) This is called the liar's paradox, and it’s the basic idea behind the proof of Gödel's theorem. The core of the issue is that we have a system (the English language) trying to model itself, and we’ve exhibited a sentence whose interpreted meaning references that very same sentence.
The idea of Gödel's proof is to encode a “provability version” of the liar's paradox into number theory. That is, given a formal system rich enough to model number theory, Gödel comes up with a string G of the system whose meaning under interpretation is: “G is not provable.” If G were false, then G would be provable and hence true, a contradiction. So G must be true, making it an unprovable truth. It follows that the formal system in question is incomplete.
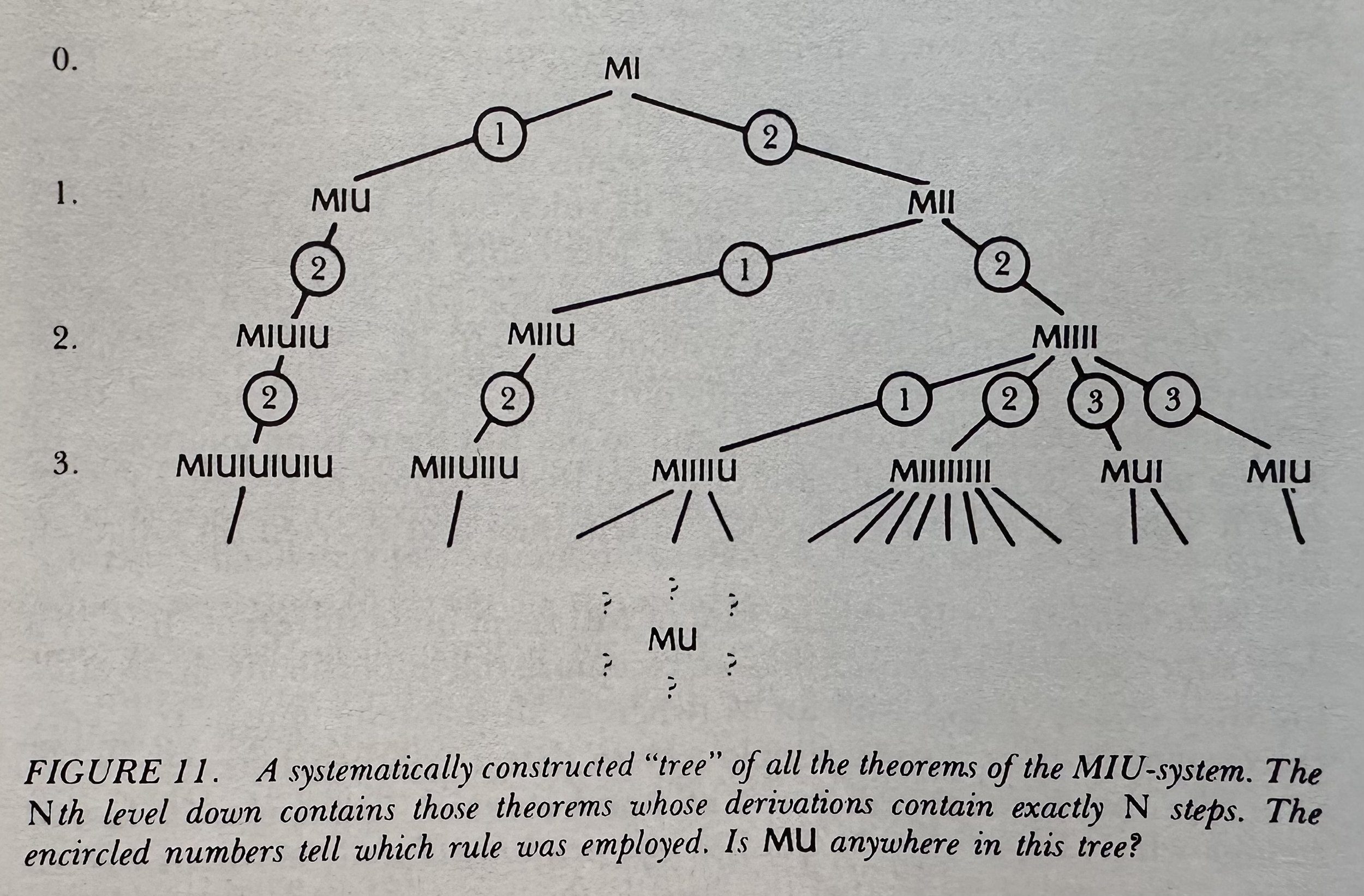
Gödel numbering system: M = 3, I = 1, U = 0. Therefore, MIUUI = 31001.
The procedure above turned strings of the MIU-system into numbers, and claims about those strings into statements of number theory. This is called Gödel numbering, and it can be done to any formal system. Via Gödel numbering, the claim "MU is a theorem" about the MIU-system corresponds to the number-theoretical claim "30 is a MIU-number.” In other words, despite the MIU-system having no interpretation that gives its strings meaning, Gödel numbering gives number-theoretical meaning to certain claims about the MIU-system.
In GEB, Hofstadter spends two chapters constructing an explicit example of a formal system that models number theory, called Typographical Number Theory, or TNT (foreshadowing that it will blow itself up). For the sake of concreteness, he then proves the Incompleteness Theorem for the system TNT.
___________________________________________________________________________
Intro: A Musico-Logical Offering
Summary- Introduction: A Musico-Logical Offering: The book opens with the story of Bach's Musical Offering. Bach made an impromptu visit to King Frederick the Great of Prussia, and was requested to improvise upon a theme presented by the King. His improvisations formed the basis of that great work. The Musical Offering and its story form a theme upon which I "improvise" throughout the book, thus making a sort of "Metamusical Offering". Self-reference and the interplay between different levels in Bach are discussed; this leads to a discussion of parallel ideas in Escher's drawings and then Gödel's Theorem. A brief presentation of the history of logic and paradoxes is given as background for Gödel's Theorem. This leads to mechanical reasoning and computers, and the debate about whether AI is possible. I close with an explanation of the origins of the book—particularly the why and wherefore of the Dialogues.
Piano Forte (Soft-Loud): Developed in the early 18c as a modification of the harpsichord. The problem with the harpsichord was that pieces could only be played at a rather uniform loudness- there was no way to strike one note more loudly than its neighbors. The “soft-loud”, as its name implies, provided a remedy to this problem. From Italy, where Bartolomeo Cristofori had made the first one, the soft-loud idea had spread widely.
The idea of a Canon is that one single theme is played against itself…A Fugue is like a canon, in that it is usually based on one theme which gets played in different speeds or upside down or backwards. However, the notion of fugue is much less rigid than that of canon, and consequently it allows for more emotional and artistic expression. The telltale sign of a fugue is the way it begins: with a single voice singing its theme. When it is done, then a second voice enters, either five scale-notes up, or four down. Meanwhile the first voice goes on, singing the “countersubject”: a secondary theme, chosen to provide rhythmic, harmonic, and melodic contrasts to the subject. Each of the voices enters in turn, singing the theme, often to the accompaniment of the countersubject in some other voice, with the remaining voices doing whatever fanciful things entered the composer’s mind.
Strange Loops: A phenomenon that occurs whenever, by moving upwards (or downwards) through the levels of some hierarchical system, we unexpectedly find ourselves right back where we started.
Tangled Hierarchy: A system in which a strange loop occurs.
Epimenides Paradox: All Cretans are liars- “I am lying”- this statement is false (Epimenides was a Cretan).
Gödel’s Theorem: Appears as proposition VI in his 1931 paper “On Formally Undecidable Propositions in Principa Mathematica and related System I. It states “All consistent axiomatic formulations of number theory include undecidable propositions.”
In short, Gödel showed that provability is a weaker notion than truth, no matter what axiomatic system is involved.
Gödel’s theorem shows that no fixed system, no matter how complicated, could represent the complexity of the whole numbers: 0, 1, 2, 3….
“The following sentence is false. The preceding sentence is true.”
The final irony of it all is that the proof of Gödel’s Incompleteness Theorem involved importing the Epimenides paradox right into the heart of PM, a bastion supposedly invulnerable to the attacks of Strange Loops! Although Gödel’s strange loop did not destroy PM, it made it far less interesting to mathematicians, for it showed that Russell and Whitehead’s original aims were illusory.
Essential abilities for intelligence:
To respond to situations very flexibly; to take advantage of fortuitous circumstances; to make sense out of ambiguous or contradictory messages; to recognize the relative importance of different elements of situation.
To find similarities between situations despite differences which may separate them.
To draw distinctions between situations despite similarities which may link them.
To synthesize new concepts by taking old concepts and putting them together in new ways.
To come up with ideas which are novel.
Here one runs up against a seeming paradox. Computers by their very nature are the most inflexible, desireless, rule-following of beasts. Fast though they may be, they are nonetheless the epitome of unconsciousness. How, then, can intelligent behavior be programmed? Isn't this the most blatant of contradictions in terms? One of the major theses of this book is that it is not a contradiction at all. One of the major purposes of this book is to urge each reader to confront the apparent contradiction head on, to savor it, to turn it over, to take it apart, to wallow in it, so that in the end the reader might emerge with new insights into the seemingly unbreachable gulf between the formal and the informal, the animate and the inanimate, the flexible and the inflexible. This is what AI research is all about. And the strange flavor of AI work is that people try to put together long sets of rules in strict formalisms which tell inflexible machines how to be flexible.
___________________________________________________________________________
Three Part Invention
Summary- Three-Part Invention: Bach wrote 15x three-part inventions. In this three-part Dialogue, the Tortoise and Achilles- the main fictional protagonists in the Dialogues- are "invented" by Zeno (as in fact they were, to illustrate Zeno's paradoxes of motion). Very short, it simply gives the flavor of the Dialogues to come.
Zeno’s Theorem: “Motion Unexists.”
___________________________________________________________________________
Ch. 1: The MU-puzzle
Summary- Chapter I: The MU-puzzle: A simple formal system (the MIU-system) is presented, and the reader is urged to work out a puzzle to gain familiarity with formal systems in general. A number of fundamental notions are introduced: string, theorem, axiom, rule of inference, derivation, formal system, decision procedure, working inside/outside the system.
The formal system I use was invented by the American logician Emil Post in the 1920s, and is often called a Post Production system.
Theorem: A statement in ordinary language which somebody once proved to be true by some sort of logical argument.
theorem: (uncapitalized) a string producible in some formal system.
Rules of Production (Inference): Symbol-shunting rules present in all formal systems.
It is possible to program a machine to do a routine task in such a way that the machine will never notice even the most obvious facts about what it is doing; but it is inherent in human consciousness to notice some facts about the things one is doing. It is possible for a machine to act unobservant; it is impossible for a human to act unobservant.
The property of being unobservant seems to be the characteristic feature of machines.
Mechanical mode (M-mode).
Intelligent mode (I-mode).
Un-mode (U-mode): A Zen way of approaching things.
___________________________________________________________________________
Two Part Invention
Summary- Two-Part Invention: Bach wrote 15x two-part inventions. This two-part Dialogue was written not by me, but by Lewis Carroll in 1895. Carroll borrowed Achilles and the Tortoise from Zeno, and I in turn borrowed them from Carroll. The topic is the relation between reasoning, reasoning about reasoning, and so on. It parallels, in a way, Zeno's paradoxes about the impossibility of motion, seeming to show, by using infinite regress, that reasoning is impossible. It is a beautiful paradox, and is referred to several times later in the book.
Euclid’s First Proposition: 1) Things that are equal to the same are equal to each other; 2) The two sides of this triangle are things that are equal to the same; 3) The two sides of this triangle are equal to each other.
___________________________________________________________________________
Ch. II: Meaning and Form in Mathematics
Summary- Chapter Il: Meaning and Form in Mathematics: A new formal system (the pq-system) is presented, even simpler than the MIU-system of Chapter I. Apparently meaningless at first, its symbols are suddenly revealed to possess meaning by virtue of the form of the theorems they appear in. This revelation is the first important insight into meaning: its deep connection to isomorphism. Various issues related to meaning are then discussed, such as truth, proof, symbol manipulation, and the elusive concept, "form".
Isomorphism: An information preserving transformation.
pq-system: p = plus, q = equals, - = 1, -- = 2, --- = 3.
The pq-system seems to forces us into recognizing that symbols of a formal system, though initially without meaning, cannot avoid taking on “meaning” of sorts, at least if an isomorphism is found.
Learning grammar is like learning math (me).
The idea of well-formed strings in any formal system is that they are those strings which, when interpreted symbol by symbol, yield grammatical sentences.
Euclid’s Theorem: There are infinitely many prime numbers.
In Math, the goal is always to give an ironclad proof for some unobvious statement.
In chapters to come, we will lay out a formal system that 1) includes a stylized vocabulary in which all statement about natural numbers can be expressed, and 2) has rules corresponding to all the types of reasoning which seem necessary. A very important question will be whether the rules for symbol manipulation which we have then formulated are really of equal power (as far as number theory is concerned) to our usual mental reasoning abilities- or, more generally, whether it is theoretically possible to attain the level of our thinking abilities, by using some formal system.
___________________________________________________________________________
Sonata for Unaccompanied Achilles
Summary- Sonata for Unaccompanied Achilles: A Dialogue which imitates the Bach Sonatas for unaccompanied violin. In particular, Achilles is the only speaker, since it is a transcript of one end of a telephone call, at the far end of which is the Tortoise. Their conversation concerns the concepts of "figure" and "ground" in various contexts- e.g., Escher's art. The Dialogue itself forms an example of the distinction, since Achilles' lines form a "figure", and the Tortoise's lines-implicit in Achilles' lines-form a "ground".
___________________________________________________________________________
Ch. III: Figure and Ground
Summary- Chapter Ill: Figure and Ground: The distinction between figure and ground in art is compared to the distinction between theorems and nontheorems in formal systems. The question "Does a figure necessarily contain the same information as its ground?" leads to the distinction between recursively enumerable sets and recursive sets.
Recursively Enumerable (r.e.): Sets of strings that can be generated according to typographical rules.
There exist formal systems whose negative space (set of non-theorems) is not the positive space (set of theorems) of any formal system- there exist recursively enumerable sets which are not recursive.
___________________________________________________________________________
Contracrostipunctus
Summary- Contracrostipunctus: This Dialogue is central to the book, for it contains a set of paraphrases of Gödel's self-referential construction and of his Incompleteness Theorem. One of the paraphrases of the Theorem says, "For each record player there is a record which it cannot play." The Dialogue's title is a cross between the word "acrostic" and the word "contrapunctus", a Latin word which Bach used to denote the many fugues and canons making up his Art of the Fugue. Some explicit references to the Art of the Fugue are made. The Dialogue itself conceals some acrostic tricks.
Gödel’s Incompleteness Theorem (1931): In any reasonable mathematics system, there will always be true statements that cannot be proved.
Acrostics: Poems which conceal messages.
___________________________________________________________________________
Ch. IV: Consistency, Completeness, and Geometry
Summary- Chapter IV: Consistency, Completeness, and Geometry: The preceding Dialogue is explicated to the extent it is possible at this stage. This leads back to the question of how and when symbols in a formal system acquire meaning. The history of Euclidean and non-Euclidean geometry is given, as an illustration of the elusive notion of "undefined terms". This leads to ideas about the consistency of different and possibly "rival" geometries. Through this discussion the notion of undefined terms is clarified, and the relation of undefined terms to perception and thought processes is considered.
The fact that truth transcends theoremhood, in any given formal system, is called “incompleteness” of that system.
300 BCE: Euclid’s pens “Elements” as a compilation of all of what was known about plane and solid geometry:
A straight-line segment can be drawn joining any two points.
Any straight-line segment can be extended indefinitely in a straight line.
Given any straight-line segment, a circle can be drawn having the segments as radius and one end point as center.
All right angles are congruent.
If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.
Consistency: Every theorem, when interpreted, becomes a true statement. Consistency is not a property of a formal system per se, but depends on the interpretation which is proposed for it.
Inconsistency: Occurs when there is at least one false statement among the interpreted theorems.
A system would be internally inconsistent if it contains two or more theorems whose interpretations were incompatible with one another, and internally consistent if all interpreted theorems were compatible with one another.
A system-plus-interpretation would be logically consistent just as long as no two of its theorems, when interpreted as statements, directly contradict each other; and mathematically consistent just as long as interpreted theorems do not violate mathematics; and physically consistent just as long as all its interpreted theorems are compatible with physical law; then comes biological consistent), and so on.
If consistency is the minimal condition under which symbols acquire passive meanings, then its complementary notion, completeness, is the maximal confirmation of those passive meanings.
Einstein’s general relativity said that the geometry of the universe is determined by its content of matter.
___________________________________________________________________________
Little Harmonic Labyrinth
Summary- Little Harmonic Labyrinth: This is based on the Bach organ piece by the same name. It is a playful introduction to the notion of recursive- i.e., nested- structures. It contains stories within stories. The frame story, instead of finishing as expected, is left open, so the reader is left dangling without resolution. One nested story concerns modulation in music- particularly an organ piece which ends in the wrong key, leaving the listener dangling without resolution.
God over Djinn (GOD).
___________________________________________________________________________
Ch. V: Recursive Structures and Processes
Summary- Chapter V: Recursive Structures and Processes: The idea of recursion is presented in many different contexts: musical patterns, linguistic patterns, geometric structures, mathematical functions, physical theories, computer pro-grams, and others.
Recursion: Defining a problem in terms of itself (which creates an infinite loop of attempting to solve the problem (recursion requires a stopping condition).
The whole world is built out of recursion. No particle can even be defined without referring to all other particles, whose definitions in turn depend on the first particles, etc. Round and round, in a never-ending loop.
A recursive definition (when properly formulated) never leads to infinite regress or paradox. This is because a recursive definition never defines something in terms of itself, but always in terms of simpler versions of itself.
Push: To suspend operations on the task you're currently working on, without forgetting where you are- and to take up a new task. The new task is usually said to be "on a lower level" than the earlier task.
Pop: The reverse of push; to close operations on one level, and to resume operations exactly where you left off, one level higher.
Stack: A table telling you such things as (1) where you were in each unfinished task (jargon: the "return address"), (2) what the relevant facts to know were at the points of interruption (jargon: the "variable bindings").
Recursive Transition Network (RTN): A diagram showing various paths which can be followed to accomplish a particular task. Each path consists of a number of nodes, or little boxes with words in them, joined by arcs, or lines with arrows.
Modularization: The breaking-up of a task into natural subtasks.
Loops: Perform some series of related steps over and over, and abort the process when specific conditions are met.
Free loop: Dangerous, because the criterion for abortion may never occur, leaving the computer in a so-called "infinite loop.”
Augmented Transition Network (ATN): An RTN which has been souped up with parameters and conditions that control the choice of pathways inside it.
Hofstadter's Law: It always takes longer than you expect, even when you take into account Hofstadter's Law.
Recursively Enumerative (r.e.): A set that can be generated from a set of starting points (axioms), by the repeated application of rules of inference. Thus, the set grows and grows, each new element being compounded somehow out of previous elements, in a sort of "mathematical snowball.”
Fibonacci numbers and the Lucas numbers are perfect examples of r.e. sets- snowballing from two elements by a recursive rule into infinite sets.
Recursive Enumeration: A process in which new things emerge from old things by fixed rules. The further out you go, the less predictable they get. This kind of thought carried a little further suggests that suitably complicated recursive systems might be strong enough to break out of any predetermined patterns. And isn't this one of the defining properties of intelligence? Instead of just considering programs composed of procedures which can recursively call themselves, why not get really sophisticated, and invent programs which can modify themselves-programs which can act on programs, extending them, improving them, generalizing them, fixing them, and so on? This kind of "tangled recursion" probably lies at the heart of intelligence.
___________________________________________________________________________
Canon by Intervallic Augmentation
Summary- Canon by Intervallic Augmentation: Achilles and the Tortoise try to resolve the question, "Which contains more information—a record, or the phonograph which plays it?" This odd question arises when the Tortoise describes a single record which, when played on a set of different phonographs, produces two quite different melodies: B-A-C-H and C-A-G-E. It turns out, however, that these melodies are "the same", in a peculiar sense.
___________________________________________________________________________
Ch. VI: The Location of Meaning
Summary- Chapter VI: The Location of Meaning: A broad discussion of how meaning is split among coded message, decoder, and receiver. Examples presented include strands of DNA, undeciphered inscriptions on ancient tablets, and phonograph records sailing out in space. The relationship of intelligence to "absolute" meaning is postulated.
Meaning could not be said to be located in any single place, nor could it be said that a message has any universal, or objective, meaning, since each observer could bring its own meaning to each message.
Isomorphism: (iso- equal, morphosis- to form or shape; Greek); a map that preserves sets and relations among elements (Wolfram).
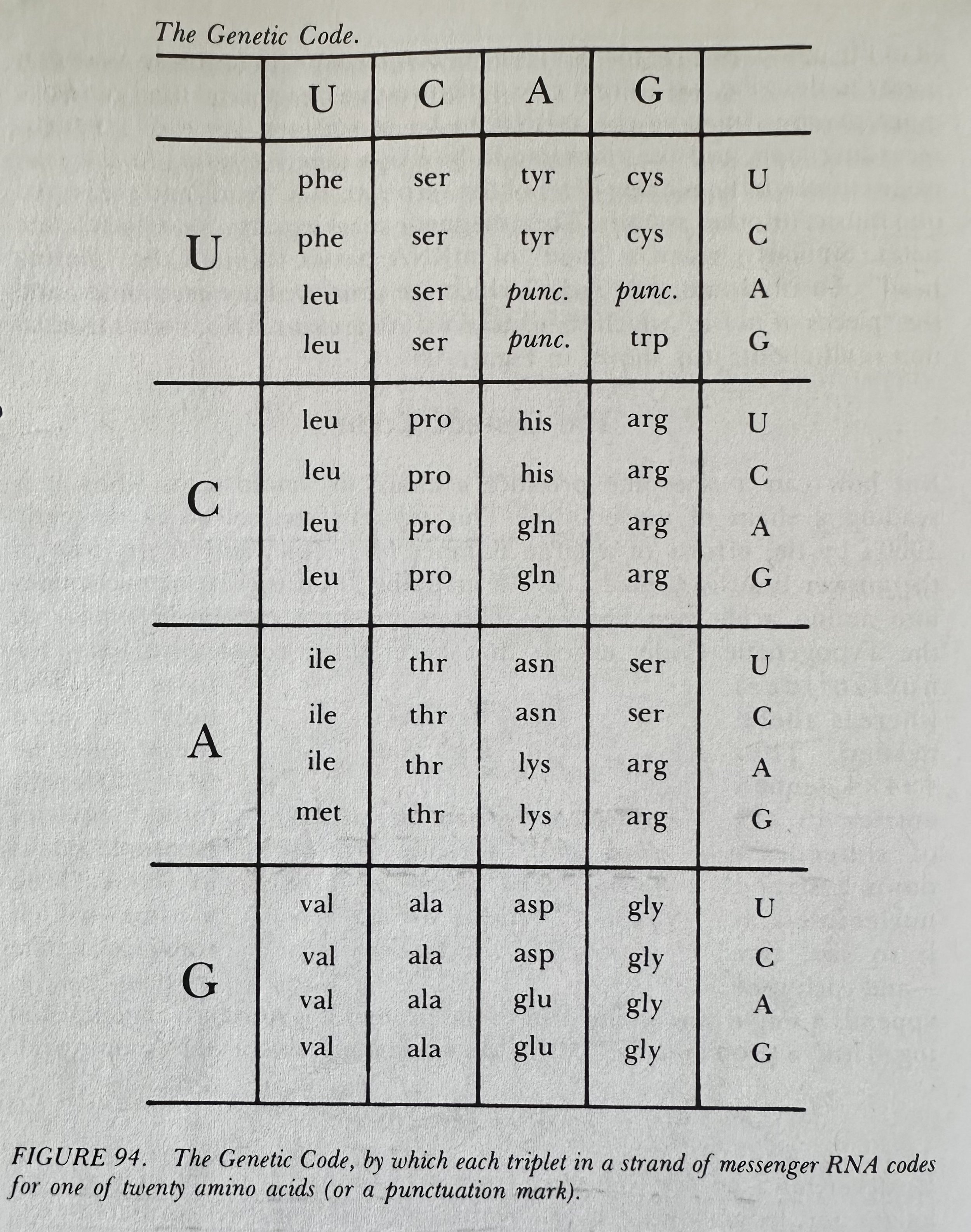
Genetic Code: Instructions for translating short portions of DNA into various amino acids.
Cracking the Genetic Code is comparable to figuring out the phonetic values of the letters of a foreign alphabet, without figuring out the grammar of the language or the meanings of any of its words. The cracking of the Genetic Code was a vital step on the way to extracting the meaning of DNA strands, but it was only the first on a long path which is yet to be trodden.
Rosetta Stone: Contains parallel text in three ancient scripts: hieroglyphics, demotic characters, and Greek. The inscription on this basalt stele was first deciphered in 1821 by Jean François Champollion, the "father of Egyptology"; it is a decree of priests assembled at Memphis in favor of Ptolemy V Epiphanes.
Three parts to a message
Frame Message: "I am a message; decode me if you can!"; and it is implicitly conveyed by the gross structural aspects of any information-bearer. To understand the frame message is to recognize the need for a decoding-mechanism. If the frame message is recognized as such, then attention is switched to the outer message.
Outer Message: information, implicitly carried by symbol-patterns and structures in the message, which tells how to decode the inner message. To understand the outer message is to build, or know how to build, the correct decoding mechanism for the inner message
Inner Message: it is the message which is supposed to be transmitted: the emotional experiences in music, the phenotype in genetics, the royalty and rites of ancient civilizations in tablets, etc. To understand the inner message is to have extracted the meaning intended by the sender.
Jukebox Theory of Meaning: The doctrine that no message contains inherent meaning, because, before any message can be understood, it has to be used as the input to some "jukebox"', which means that information contained in the "jukebox" must be added to the message before it acquires meaning.
This argument is similar to the trap which the Tortoise caught Achilles in, in Lewis Carroll's Dialogue. There, the trap was the idea that before you can use any rule, you have to have a rule which tells you how to use that rule; in other words, there is an infinite hierarchy of levels of rules, which prevents any rule from ever getting used.
Music has three major dimensions of structure (melody, harmony, rhythm), each of which can be further divided into small-scale, intermediate, and overall aspects.
___________________________________________________________________________
Chromatic Fantasy, and Feud
Summary- Chromatic Fantasy, And Feud: A short Dialogue bearing hardly any resemblance, except in title, to Bach's Chromatic Fantasy and Fugue. It concerns the proper way to manipulate sentences so as to preserve truth-and in particular the question of whether there exist rules for the usage of the word "and". This Dialogue has much in common with the Dialogue by Lewis Carroll.
“I'm a peaceful soul, bothering nobody and leading a gentle, herbivorous life.”-Tortoise.
___________________________________________________________________________
Ch. VII: The Propositional Calculus
Summary- Chapter VII: The Propositional Calculus: It is suggested how words such as "and" can be governed by formal rules. Once again, the ideas of isomorphism and automatic acquisition of meaning by symbols in such a system are brought up. All the examples in this Chapter, incidentally, are "Zentences"- sentences taken from Zen köans. This is purposefully done, somewhat tongue-in-cheek, since Zen köans are deliberately illogical stories.
Carry Over Rule: Inside a fantasy, any theorem from the "reality" one level higher can be brought in and used.
One day Tokusan told his student Ganto, "I have two monks who have been here for many years. Go and examine them." Ganto picked up an ax and went to the hut where the two monks were meditating. He raised the ax, saying, "If you say a word I will cut off your heads; and if you do not say a word, I will also cut off your heads."
“You can't go on defending your patterns of reasoning forever. There comes a point where faith takes over.”-Lewis Carroll.
One can never give an ultimate, absolute proof that a proof in some system is correct. Of course, one can give a proof of a proof, or a proof of a proof of a proof-but the validity of the outermost system always remains an unproven assumption, accepted on faith. One can always imagine that some unsuspected subtlety will invalidate every single level of proof down to the bottom, and that the "proven" result will be seen not to be correct after all.
Fallacies can result if you fail to distinguish carefully between working in the system (the M-mode) and thinking about the system (the I-mode).
Proof: An informal product of normal thought, written in a human language, for human consumption. All sorts of complex features of thought may he used in proofs, and, though they may "feel right", one may wonder if they can be defended logically. That is really what formalization is for.
Derivation: An artificial counterpart of a proof, and its purpose is to reach the same goal but via a logical structure whose methods are not only all explicit, but also very simple.
Each type of simplicity, however, brings along a characteristic type of complexity.
___________________________________________________________________________
Crab Canon
Summary- Crab Canon: A Dialogue based on a piece by the same name from the Musical Offering. Both are so named because crabs (supposedly) walk backwards. The Crab makes his first appearance in this Dialogue. It is perhaps the densest Dialogue in the book in terms of formal trickery and level-play. Gödel, Escher, and Bach are deeply intertwined in this very short Dialogue.
___________________________________________________________________________
Ch. VIII: Typographical Number Theory
Summary- Chapter VIII: Typographical Number Theory: An extension of the Propositional Calculus called "TNT" is presented. In TNT, number-theoretical reasoning can be done by rigid symbol manipulation. Differences between formal reasoning and human thought are considered.
The interpretation of Axiom 1- "Zero is not the successor of any natural number"—is one of five famous properties of natural numbers first explicitly recognized by the mathematician and logician Giuseppe Peano, in 1889.
___________________________________________________________________________
A Mu Offering
Summary- A Mu Offering: This Dialogue foreshadows several new topics in the book. Ostensibly concerned with Zen Buddhism and köans, it is actually a thinly veiled discussion of theoremhood and non-theoremhood, truth and falsity, of strings in number theory. There are fleeting references to molecular biology —particularly the Genetic Code. There is no close affinity to the Musical Offering, other than in the title and the playing of self-referential games.
Zen is a kind of Buddhism which was founded by a monk named Bodhidharma, who left India and went to China around the 6c. Bodhidharma was the first patriarch. About 500 yrs later, Zen was brought to Japan, and it took hold very well there. Since that time, it has been one of the principal religions in Japan.
In Zen, one seeks enlightenment, or ‘satori’, the state of “no-mind.” In this state, one does not think about the world, one just IS.
It seems to me that you may begin approaching Zen through any path you know- even if it is completely antithetical to Zen. As you approach it, you gradually learn to stray from that path. The more you stray from the path, the closer you get to Zen.
Köans: Zen parables; a story about Zen masters and their students. Sometimes it is like a riddle; other times like a fable.
“Just chalk it up to my unenlightened state.”-Tortoise.
___________________________________________________________________________
Ch. IX: Mumon and Gödel
Summary- Chapter IX: Mumon and Gödel: An attempt is made to talk about the strange ideas of Zen Buddhism. The Zen monk Mumon, who gave well known commentaries on many köans, is a central figure. In a way, Zen ideas bear a metaphorical resemblance to some contemporary ideas in the philosophy of mathematics. After this "Zennery", Gödel's fundamental idea of Gödel-numbering is introduced, and a first pass through Gödel's Theorem is made.
In general, the Zen attitude is that words and truth are incompatible, or at least that no words can capture truth.
The monk Mumon ("No-gate"), in the 13c, compiled 48 köans, following each with a commentary and a small "poem. This work is called "The Gateless Gate" or the Mumonkan ("No-gate barrier").
Only by stepping outside of logic, so the theory goes, can one make the leap to enlightenment.
Dualism: The conceptual division of the world into categories.
Perhaps the most concise summary of enlightenment would be: transcending dualism.
It is perhaps wrong to say that the enemy of enlightenment is logic; rather, it is dualistic, verbal thinking.
If holism claims that things can only be understood as wholes, not as sums of their parts, Zen goes one further, in maintaining that the world cannot be broken into parts at all.
The Zen monk Bassui wrote a letter to one of his disciples who was about to die, and in it he said: "Your end which is endless is as a snowflake dissolving in the pure air." The snowflake, which was once very much a discernible subsystem of the universe, now dissolves into the larger system which once held it. Though it is no longer present as a distinct subsystem, its essence is somehow still present, and will remain so.
“Ism” is an anti-philosophy, a way of being without thinking.
The Buddhist allegory of "Indra's Net" tells of an endless net of threads throughout the universe, the horizontal threads running through space, the vertical ones through time. At every crossing of threads is an individual, and every individual is a crystal bead. The great light of "Absolute Being " illuminates and penetrates every crystal bead; moreover, every crystal bead reflects not only the light from every other crystal in the net-but also every reflection of every reflection throughout the universe.
“Enlightenment always comes after the road of thinking is blocked.”
Just concentrate your whole energy into this MU, and do not allow any discontinuation. When you enter this MU and there is no discontinuation, your attainment will be as a candle burning and illuminating the whole universe.
Central Dogma of Mathematical Logic, and depicting it in a two-step diagram: TNT N → meta-TNT In words: a string of TNT has an interpretation in N; and a statement of N may have a second meaning as a statement about TNT.
___________________________________________________________________________
---Part 2---
Part II claims that the ideas of part I have to do with AI and the nature of consciousness (Sam Marks, 2021).
___________________________________________________________________________
Prelude…
Summary- Prelude...: This Dialogue attaches to the next one. They are based on preludes and fugues from Bach's Well-Tempered Clavier. Achilles and the Tortoise bring a present to the Crab, who has a guest: the Anteater. The present turns out to be a recording of the W.T.C.; it is immediately put on. As they listen to a prelude, they discuss the structure of preludes and fugues, which leads Achilles to ask how to hear a fugue: as a whole, or as a sum of parts? This is the debate between holism and reductionism, which is soon taken up in the Ant Fugue.
a^n + b^n = c^n: there are no solutions for n > 2. the Theorem has been proven for many specific values of n—in particular, all n up to 125,000.
“I'd certainly like to offer my own meager knowledge, if it might prove of some assistance.”
"What is the right way to listen to a fugue: as a whole, or as the sum of its parts?"
___________________________________________________________________________
Ch. X: Levels of Description, and Computational Systems
Summary- Chapter X: Levels of Description, and Computer Systems: Various levels of seeing pictures, chessboards, and computer systems are discussed. The last of these is then examined in detail. This involves describing machine languages, assembly languages, compiler languages, operating systems, and so forth. Then the discussion turns to composite systems of other types, such as sports teams, nuclei, atoms, the weather, and so forth. The question arises as to how many intermediate levels exist- or indeed whether any exist.
Intelligence depends crucially on the ability to create high-level descriptions of complex arrays, such as chess boards, television screens, printed pages, or paintings.
A bit is just a magnetic "switch" that can be in either of two positions.
Compiler: Takes input (i.e., a finished Algol program) and produces output (a long sequence of machine language instructions). At this point, the compiler has done its duty. The output is then given to the computer to run.
Interpreter: Constantly running while the programmer types in one LISP statement after another, and each one gets executed then and there. But this doesn't mean that each statement gets first translated, then executed, for then an interpreter would be nothing but a line-by-line compiler. Instead, in an interpreter, the operations of reading a new line, "understanding" it, and executing it are intertwined: they occur simultaneously.
Sophisticated operating systems carry out similar traffic-handling and level-switching operations with respect to users and their programs. It is virtually certain that there are somewhat parallel things which take place in the brain: handling of many stimuli at the same time; decisions of what should have priority over what and for how long; instantaneous "interrupts" caused by emergencies or other unexpected occurrences; and so on.
To suggest ways of reconciling the software of mind with the hardware of brain is a main goal of this book.
System: A group of interacting parts. In most systems that we know, the parts retain their identities during the interaction, so that we still see the parts inside the system.
Superconductivity: Resistance- free flow of electrons in certain solids, at extremely low temperatures.
A nuclear physicist can proceed with theories of nuclei that are based on protons and neutrons, and ignore quark theories and their rivals. The nuclear physicist has a chunked picture of protons and neutrons- a description derived from lower-level theories but which does not require understanding the lower-level theories. Likewise, an atomic physicist has a chunked picture of an atomic nucleus derived from nuclear theory. Then a chemist has a chunked picture of the electrons and their orbits, and builds theories of small molecules, theories which can be taken over in a chunked way by the molecular biologist, who has an intuition for how small molecules hang together, but whose technical expertise is in the field of extremely large molecules and how they interact. Then the cell biologist has a chunked picture of the units which the molecular biologist pores over, and tries to use them to account for the ways that cells interact. The point is clear. Each level is, in some sense, "sealed off" from the levels below it.
In using chunked high-level models, we sacrifice determinism for simplicity.
Chunked Model: Defines a "space" within which behavior is expected to fall, and specifies probabilities of its falling in different parts of that space.
___________________________________________________________________________
…Ant Fugue
Summary- ... Ant Fugue: An imitation of a musical fugue: each voice enters with the same statement. The theme-holism versus reductionism- is introduced in a recursive picture composed of words composed of smaller words, etc. The words which appear on the four levels of this strange picture are "HOLISM", "REDUCTIONISM", and "MU". The discussion veers off to a friend of the Anteater's- Aunt Hillary, a conscious ant colony. The various levels of her thought processes are the topic of discussion. Many fugal tricks are ensconced in the Dialogue. As a hint to the reader, references are made to parallel tricks occurring in the fugue on the record to which the foursome is listening. At the end of the Ant Fugue, themes from the Prelude return, transformed considerably.
Holism is the most natural thing in the world to grasp. It's simply the belief that "the whole is greater than the sum of its parts". No one in his right mind could reject holism. Anteater: REDUCTIONISM is the most natural thing in the world to grasp. It's simply the belief that "a whole can be understood completely if you understand its parts, and the nature of their 'sum'".
You see, "MU" is an ancient Zen answer which, when given to a question, UNASKS the question. Here, the question seems to be, "Should the world be understood via holism, or via reductionism?" And the answer of "MU" here rejects the premises of the question, which are that one or the other must be chosen. By unasking the question, it reveals a wider truth: that there is a larger context into which both holistic and reductionistic explanations fit.
Each neuron receives signals from neurons attached to its input lines, and if the sum total of inputs at any moment exceeds a critical threshold, then that neuron will fire and send its own output pulse rushing off to other neurons, which may in turn fire and on down the line it goes.
What comes out of all this neural structure, and natural law? It makes what I consider my SELF sound at best like a by-product of an organism governed by natural law, and at worst, an artificial notion produced by my distorted perspective. In other words, you make me feel like I don't know who- or what- I am, if anything. Tortoise: You'll come to understand much better as we go along. But Dr. Anteater-what do you make of this similarity? Anteater: I knew there was something parallel going on in the two very different systems. Now I understand it much better. It seems that group phenomena which have coherence-trail-building, for example-will take place only when a certain threshold number of ants get involved. If an effort is initiated, perhaps at random, by a few ants in some locale, one of two things can happen: either it will fizzle out after a brief sputtering start— Achilles: When there aren't enough ants to keep the thing rolling? Anteater: Exactly. The other thing that can happen is that a critical mass of ants is present, and the thing will snowball, bringing more and more ants into the picture. In the latter case, a whole "team" is brought into being which works on a single project. That project might be trail-making, or food-gathering, or it might involve nest-keeping. Despite the extreme simplicity of this scheme on a small scale, it can give rise to very complex consequences on a larger scale.
Achilles: It is interesting to me to compare the merits of descriptions at various levels of the various levels. The highest-level descriptions seem to carry the most explanatory power, in that it gives you the most intuitive picture of the ant colony, although strangely enough, it leaves out the most important part of the colony- the ants. Anteater: But you see, despite appearances, the ants are not the most important feature. Admittedly, were it not for them, the colony wouldn't exist; but something equivalent—a brain-can exist, ant-free. So, at least from a high-level point of view, the ants are dispensable. Achilles: I'm sure no ant would embrace your theory with eagerness. Anteater: Well, I never met an ant with a high-level point of view. Crab: What a counterintuitive picture you paint, Dr. Anteater. It seems that, if what you say is true, in order to grasp the whole structure, you have to describe it omitting any mention of its fundamental building blocks.
Anteater: Exactly. There is no natural mapping from the individual letters into the real world. The natural mapping occurs on a higher level-between words, and parts of the real world. If you wanted to describe the book, therefore, you would make no mention of the letter level. Achilles: Of course not! I'd describe the plot and the characters, and so forth. Anteater: So there you are. You would omit all mention of the building blocks, even though the book exists thanks to them. They are the medium, but not the message.
Anteater: What about your OWN brain? Aren't you aware of your own thoughts? Isn't that the essence of consciousness? What else are you doing but reading your own brain directly at the symbol level? Achilles: I never thought of it that way. You mean that I bypass all the lower levels, and only see the topmost level? Anteater: That's the way it is, with conscious systems. They perceive themselves on the symbol level only, and have no awareness of the lower levels, such as the signal levels. Achilles: Does it follow that in a brain, there are active symbols which are constantly updating themselves so that they reflect the overall state of the brain itself, always on the symbol level?
Fourmi's infamous "Well-Tested Conjecture"?: 2^a + 2^b = 2^c
___________________________________________________________________________
Ch. XI: Brains & Thoughts
Summary- Chapter XI: Brains and Thoughts: "How can thoughts be supported by the hardware of the brain?" is the topic of the Chapter. An overview of the large-scale and small-scale structure of the brain is first given. Then the relation between concepts and neural activity is speculatively discussed in some detail.
The equation n^a + n^b = n^c has solutions in positive integers a, b, c, and n only when n = 2 (and then there are infinitely many triplets a, b, c which satisfy the equation); but there are no solutions for n > 2.
The most important cells in the brain are nerve cells, or neurons, of which there are ~10B. (Curiously, outnumbering the neurons by about ten to one are the glial cells, or glia. Glia are believed to play more of a supporting role to the neurons' starring role, and therefore we will not discuss them.) Each neuron possesses a number of synapses ("entry ports") and one axon ("output channel"). The input and output are electrochemical flows: that is, moving ions. In between the entry ports of a neuron and its output channel is its cell body, where "decisions" are made. The type of decision which a neuron faces- and this can take place up to 1000x/sec is this: whether or not to fire- that is, to release ions down its axon, which eventually will cross over into the entry ports of one or more other neurons, thus causing them to make the same sort of decision. The decision is made in a very simple manner: if the sum of all inputs exceeds a certain threshold, yes; otherwise, no. Some of the inputs can be negative inputs, which cancel out positive inputs coming from somewhere else. In any case, it is simple addition which rules the lowest level of the mind. To paraphrase Descartes' famous remark, "I think, therefore I sum" (from the Latin Cogito, ergo am). Now although the manner of making the decision sounds very simple, there is one fact which complicates the issue: there may be as many as 200,000 separate entry ports to a neuron, which means that up to 200,000 separate summands may be involved in determining the neuron's next action. After a neuron fires, it needs a short recovery time before firing again; characteristically this is measured in ms, so that a neuron may fire up to about a 1000x/sec.
For large amounts of information to be carried or processed, many neurons must be involved. And therefore, one might guess that larger structures, composed from many neurons, would exist, which handle concepts on a higher level. This is undoubtedly true, but the most naive assumption- that there is a fixed group of neurons for each different concept- is almost certainly false.
Cerebrum: The largest part of the brain and is divided into the left and right hemispheres. The outer few millimeters of each cerebral hemisphere are coated with a layered “bark”, or cerebral cortex. The amount of cerebral cortex is the major distinguishing feature, in terms of anatomy, between human brains and brains of less intelligent species.
Cerebellum: An area of the brain where trains of impulses are sent off to muscles to control motor activity.
Lashley’s Trials on Brain Processes: Lashley found it was not possible to find a particular region corresponding to the ability of a rat to remember the way through a maze. Instead, all the rats which had had cortex regions removed suffered some kind of impairment, and the extent of the impairment was roughly proportional to the amount of cortex taken off.
Penfield’s Trial on Brain Processes: Penfield found that the stimulation of certain neurons would reliably create specific images or sensations in the patient. These artificially provoked impressions ranged from strange but indefinable fears to buzzes and colors, and, most impressively of all, to entire successions of events recalled from some earlier time of life, such as a childhood birthday party. The set of locations which could trigger such specific events was extremely small- basically centered upon a single neuron. These results of Penfield dramatically oppose the conclusions of Lashley, since they seem to imply that local areas are responsible for specific memories, after all.
Another Explanation of Brain Processes: Another explanation would be that memories can be reconstructed from dynamic processes spread over the whole brain, but can be triggered from local spots. This theory is based on the notion of modern telephone networks, where the routing of a long-distance call is not predictable in advance, for it is selected at the time the call is placed, and depends on the situation all over the whole country. Destroying any local part of the network would not block calls; it would just cause them to be routed around the damaged area. In this sense any call is potentially nonlocalizable. Yet any call just connects up two specific points; in this sense any call is localizable.
Optical System: Retinal neurons are primarily contrast sensors. Each retinal neuron is normally firing at “cruising speed”. When its portion for the retina is struck by light, it may either fire faster or slow down and even stop firing. However, it will do so only provided that the surrounding part of the retina is less illuminated. So this means that there are two types of neuron: "on-center" ', and "off- center". On-center neurons are those whose firing rate increases whenever, in the small circular retinal area to which they are sensitive, the center is bright but the outskirts are dark. Off-center neurons are those which fire faster when there is darkness in the center and brightness in the outer ring. If an on-center pattern is shown to an off-center neuron, the neuron will slow down in firing (and vice versa). Uniform illumination will leave both types of retinal neuron unaffected; they will continue to fire at cruising speed. From the retina, signals from these neurons proceed via the optic nerve to the lateral geniculate, located somewhere towards the middle of the brain. There, one can find a direct mapping of the retinal surface in the sense that there are lateral- geniculate neurons which are triggered only by specific stimuli falling on specific areas of the retina. In that sense, the lateral geniculate is disappointing; it seems to be only a "relay station" not a further processor (although to give it its due, the contrast sensitivity seems to be enhanced in the lateral geniculate). The retinal image is coded in a straightforward way in the firing patterns of the neurons in the lateral geniculate, despite the fact that the neurons there are not arranged on a two-dimensional surface in the form of the retina, but in a three-dimensional block. So, two dimensions get mapped onto three, yet the information is preserved: an isomorphism. From the lateral geniculate, the signals proceed back to the visual cortex. Here, some new types of processing occur. The cells of the visual cortex are divided into three categories: simple, complex, and hyper-complex. Simple cells act very much like retinal cells or lateral geniculate cells: they respond to point-like light or dark spots with contrasting sur-rounds, in particular regions of the retina. Complex cells, by contrast, usually receive input from a hundred or more other cells, and they detect light or dark bars oriented at specific angles on the retina. Hyper-complex cells respond to corners, bars, or even "tongues" moving in specific directions. These latter cells are so highly specialized that they are sometimes called "higher-order hypercomplex cells".
Neural Complex/Packets/Networks/Modules: A small group of neurons that perform a well-defined module.
Symbol: A hypothetical neural complex that performs a well-defined module or task. Symbols are the hardware realizations of concepts.
Mass Communication: The transfer, among groups, of information that a single individual could not pass to another.
Each neuron, far from being a member of a unique symbol, is probably a functioning part of hundreds of symbols.
There are two basic problems in the unraveling of thought processes, as they take place in the brain. One is to explain how the low-level traffic of neuron firings gives rise to the high-level traffic of symbol activations. The other is to explain the high-level traffic of symbol activation in its own terms—to make a theory which does not talk about the low-level neural events. If this latter is possible-and it is a key assumption at the basis of all present research into AI- then intelligence can be realized in other types of hardware than brains. Then intelligence will have been shown to be a property that can be "lifted" right out of the hardware in which it resides- or in other words, intelligence will be a software property.
Our facility for making instances out of classes and classes out of instances lies at the basis of our intelligence, and it is one of the great differences between human thought and the thought processes of other animals.
Bees and other insects do not seem to have the power to generalize- that is, to develop new class symbols from instances which we would perceive as nearly identical.
You have knowledge about how you classify your own knowledge; and what is more, some of that metaknowledge may itself be stored procedurally, so that it is used without your even being aware of how it is done.
___________________________________________________________________________
English, French German Suite
Summary- English French German Suite: An interlude consisting of Lewis Carroll's nonsense poem "Jabberwocky" together with two translations: one into French and one into German, both done last century.
___________________________________________________________________________
Ch. XII: Minds and Thoughts
Summary- Chapter XII: Minds and Thoughts: The preceding poems bring up in a forceful way the question of whether languages, or indeed minds, can be "mapped" onto each other. How is communication possible between two separate physical brains? What do all human brains have in common? A geographical analogy is used to suggest an answer. The question arises, "Can a brain be understood, in some objective sense, by an outsider?"
(It’s possible that) what we call free will is a result of the interaction between the self-symbol (or subsystem), and the other symbols in the brain.
Symbols: High-level active subsystems of the brain.
It is clear that some people think more alike than others do. It would seem an obvious conclusion that there is some sort of partial software isomorphism connecting the brains of people whose style of thinking is similar- in particular, a correspondence of (1) the repertoire of symbols, and (2) the triggering patterns of symbols.
A large proportion of every human's network of symbols is universal.
Knowledge: The knowledge of facts (declarative knowledge) and knowledge of how-to's (procedural knowledge).
Consciousness: A property of a system that arises whenever there exist symbols in the system which obey triggering patterns.
Awareness: The monitoring of brain activity by a subsystem of the brain itself which seems to resemble the nearly indescribable sensation which we all know and call "consciousness"
Subsystem: A constellation of symbols, each of which can be separately activated under the control of the subsystem itself. "Subsystem" is just another name for an overgrown symbol, one which has gotten so complicated that it has many sub-symbols which interact among themselves.
It seems that the only way one could make sense of the world surrounding a localized animate object is to understand the role of that object in relation to the other objects around it. This necessitates the existence of a self-symbol; and the step from symbol to subsystem is merely a reflection of the importance of the self-symbol, and is not a qualitative change.
Most brains and all machines are, at present, "sub-critical"— they react to incoming stimuli in a stodgy and uninteresting way, have no ideas of their own, can produce only stock responses- but a few brains at present, and possibly some machines in the future, are super-critical, and scintillate on their own account. Turing suggests that it is only a matter of complexity, and that above a certain level of complexity a qualitative difference appears, so that "super-critical" machines will be quite unlike the simple ones hitherto envisaged. This may be so. Complexity often does introduce qualitative differences.
Mechanist Thesis: The idea that we can understand the operation of the whole in terms of the operations of its parts, and the operation of each part either shall be determined by its initial state and the construction of the machine, or shall be a random choice between a determinate number of determinate operations. If the mechanist produces a machine which is so complicated that this ceases to hold good of it, then it is no longer a machine for the purposes of our discussion, no matter how it was constructed.
___________________________________________________________________________
Aria with Diverse Variations
Summary- Aria with Diverse Variations: A Dialogue whose form is based on Bach's Goldberg Variations, and whose content is related to number-theoretical problems such as the Goldbach conjecture. This hybrid has as its main purpose to show how number theory's subtlety stems from the fact that there are many diverse variations on the theme of searching through an infinite space. Some of them lead to infinite searches, some of them lead to finite searches, while some others hover in between.
___________________________________________________________________________
Ch. XIII: BlooP and FlooP and GlooP
Summary- Chapter XIII: BlooP and FlooP and GlooP: These are the names of three computer languages. BlooP programs can carry out only predictably finite searches, while FlooP programs can carry out unpredictable or even infinite searches. The purpose of this Chapter is to give an intuition for the notions of primitive recursive and general recursive functions in number theory, for they are essential in Gödel's proof.
Formal systems can be difficult and unruly beasts because they have lengthening and shortening rules, which can possibly lead to never-ending searches among strings. The discovery of Gödel-numbering showed that any search for a string having a special typographical property has an arithmetical cousin: an isomorphic search for an integer with a corresponding special arithmetical property. Consequently, the quest for decision procedures for formal systems involves solving the mystery of unpredictably long searches chaos - among the integers.
Control Structure: Describes the order to do things in, when to branch back and try something again, when to skip over a set of steps, when to stop, and similar matters. It is typical of any algorithm- that is, a specific delineation of how to carry out a task- that it includes a mixture of specific operations to be performed and control statements.
Procedure: Has one input parameter, N; its output is the desired value.
Program: Consists of a chain of procedure definitions (each only calling previously defined procedures), optionally followed by one or more calls on the procedures defined.
Church-Turing (CT) Thesis: 1) What is human-computable is machine-computable, 2) What is machine-computable is FlooP- computable, 3) What is human-computable is FlooP-computable (i.e., general or partial recursive).
___________________________________________________________________________
Air on G’s String
Summary- Air on G's String: A Dialogue in which Gödel's self-referential construction is mirrored in words. The idea is due to W. V. O. Quine. This Dialogue serves as a prototype for the next Chapter.
Tortoise: Did you catch what that thing was? Achilles: Well, the whole call went like this:
Achilles: Hello?
Caller (shouting wildly): Yields falsehood when preceded by its quotation! Yields falsehood when preceded by its quotation! (Click.)
___________________________________________________________________________
Ch. XIV: On Formally Undecidable Propositions of TNT and Related Systems
Summary- Chapter XIV: On Formally Undecidable Propositions of TNT and Related Systems: This Chapter's title is an adaptation of the title of Gödel's 1931 article, in which his Incompleteness Theorem was first published. The two major parts of Gödel's proof are gone through carefully. It is shown how the assumption of consistency of TNT forces one to conclude that INT (or any similar system) is incomplete. Relations to Euclidean and non-Euclidean geometry are discussed. Implications for the philosophy of mathematics are gone into with some care.
Two key ideas which are at the core of the proof. The first key idea is the deep discovery that there are strings of TNT which can be interpreted as speaking about other strings of TNT; in short, that TNT, as a language, is capable of "introspection", or self-scrutiny. This is what comes from Gödel-numbering. The second key idea is that the property of self-scrutiny can be entirely concentrated into a single string; thus, that string's sole focus of attention is itself. This "focusing trick" is traceable, in essence, to the Cantor diagonal method.
Proof-pair: A pair of natural numbers related in a particular way.
Gödel found a simple way to express the statement "TNT is consistent" in a TNT formula; and then he showed that this formula (and all others which express the same idea) are only theorems of TNT under one condition: that TNT is inconsistent. This perverse result was a severe blow to optimists who expected that one could find a rigorous proof that mathematics is contradiction-free.
___________________________________________________________________________
Birthday Cantatatata
Summary- Birthday Cantatatata: In which Achilles cannot convince the wily and skeptical Tortoise that today is his (Achilles') birthday. His repeated but unsuccessful tries to do so foreshadow the repeatability of the Gödel argument.
Tortoise: Why, who would ever have thought you to be gullible? Quite to the contrary, I regard you as an expert in the forms of logical thought, an authority in the science of valid deductions, a fount of knowledge about correct methods of reasoning... To tell the truth, Achilles, you are, in my opinion, a veritable titan in the art of rational cogitation.
___________________________________________________________________________
Ch. XV: Jumping out of the System
Summary- Chapter XV: Jumping out of the System: The repeatability of Gödel's argument is shown, with the implication that TNT is not only incomplete, but "essentially incomplete". The fairly notorious argument by J. R. Lucas, to the effect that Gödel's Theorem demonstrates that human thought cannot in any sense be "mechanical", is analyzed and found to be wanting.
___________________________________________________________________________
Edifying Thoughts of a Tobacco Smoker
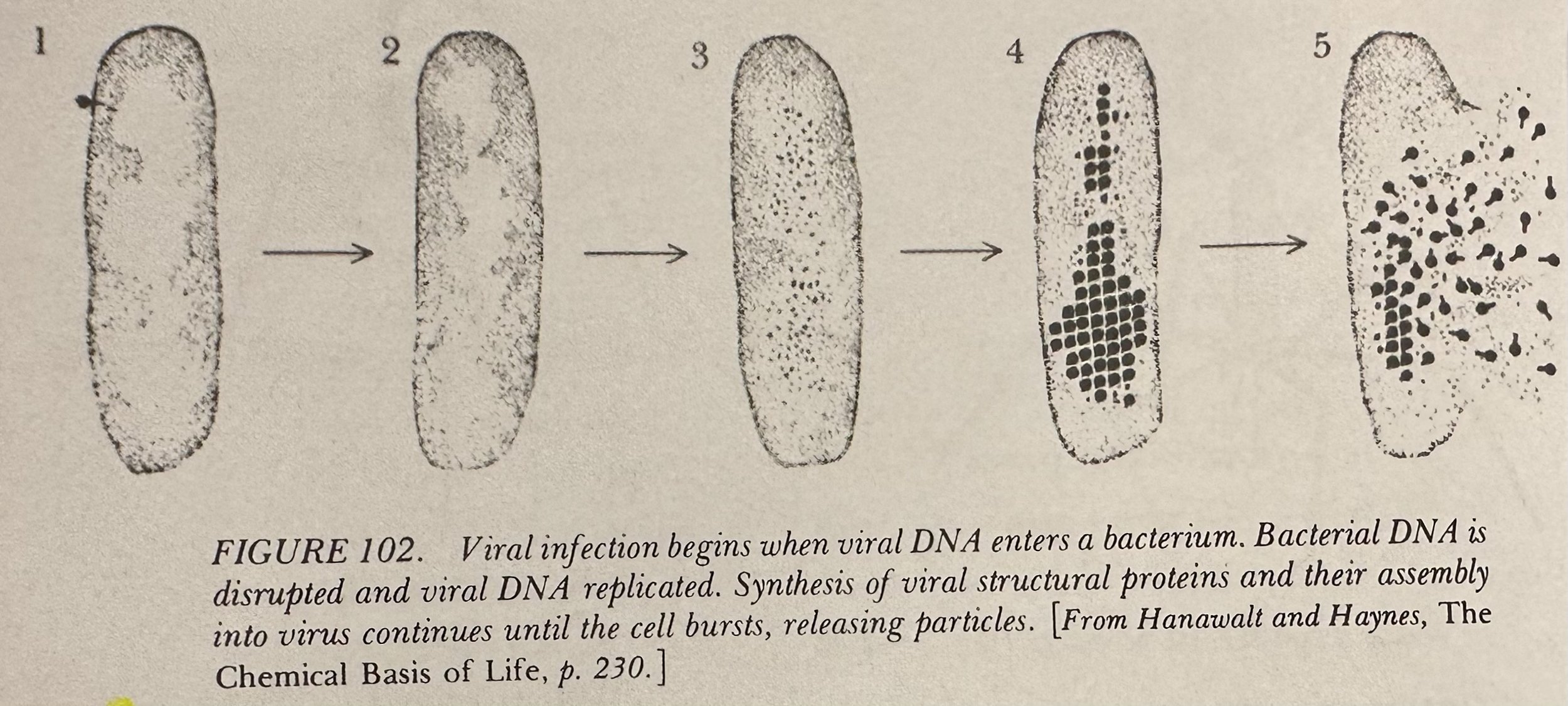
Summary- Edifying Thoughts of a Tobacco Smoker: A Dialogue treating of many topics, with the thrust being problems connected with self-replication and self-reference. Television cameras filming television screens, and viruses and other subcellular entities which assemble themselves, are among the examples used. The title comes from a poem by J. S. Bach himself, which enters in a peculiar way.
___________________________________________________________________________
Ch. XVI: Self-Ref and Self-Rep
Summary- Chapter XVI: Self-Ref and Self-Rep: This Chapter is about the connection between self-reference in its various guises, and self-reproducing entities (e.g., computer programs or DNA molecules). The relations between a self-reproducing entity and the mechanisms external to it which aid it in reproducing itself (e.g., a computer or proteins) are discussed —particularly the fuzziness of the distinction. How information travels between various levels of such systems is the central topic of this Chapter.
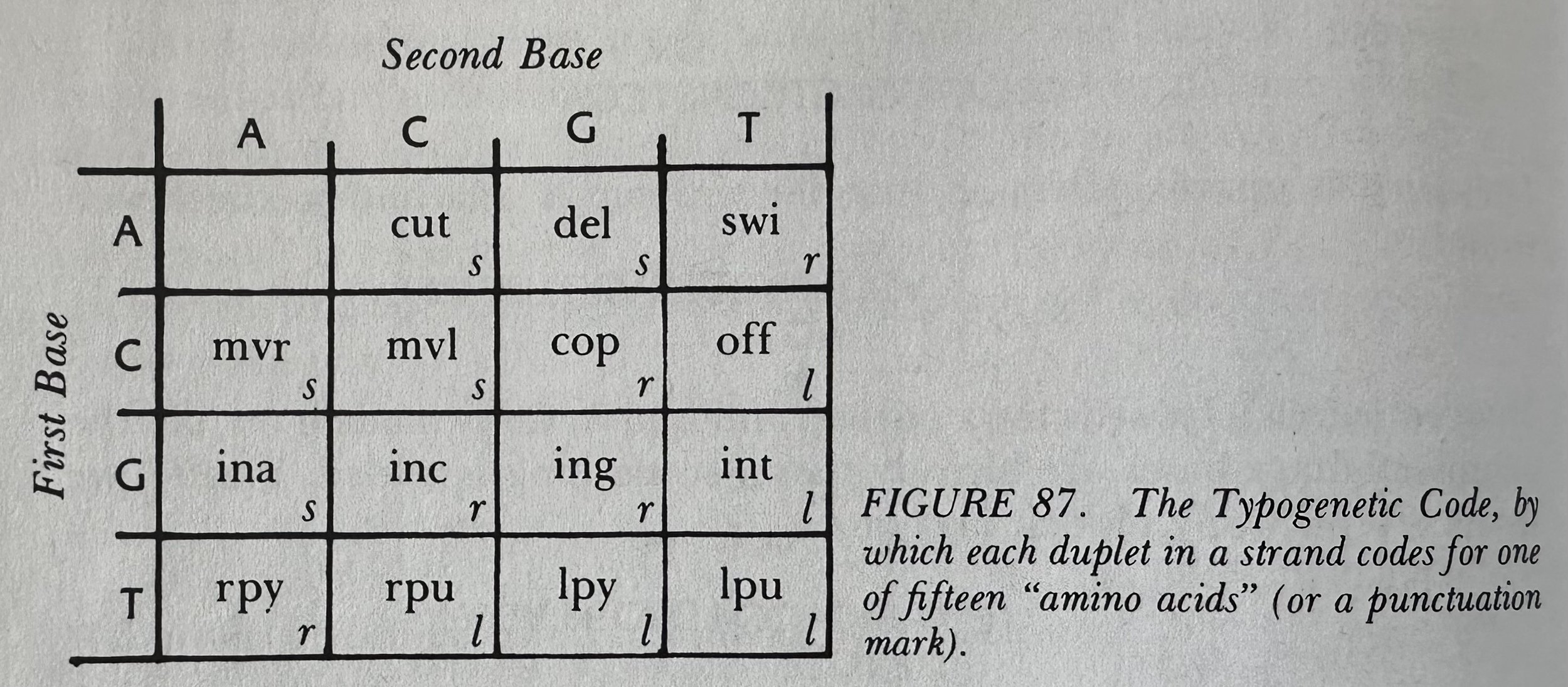
Quine Method: Self-reference by means of description instead of self-quoting or using the phrase “this sentence.”
Self-rep: Any self-referring object or entity.
Intrinsic: Dependent on a hypothesized universal notion of intelligence.
Central Dogma of Molecular Biology (Francis Crick): DNA → RNA → proteins.
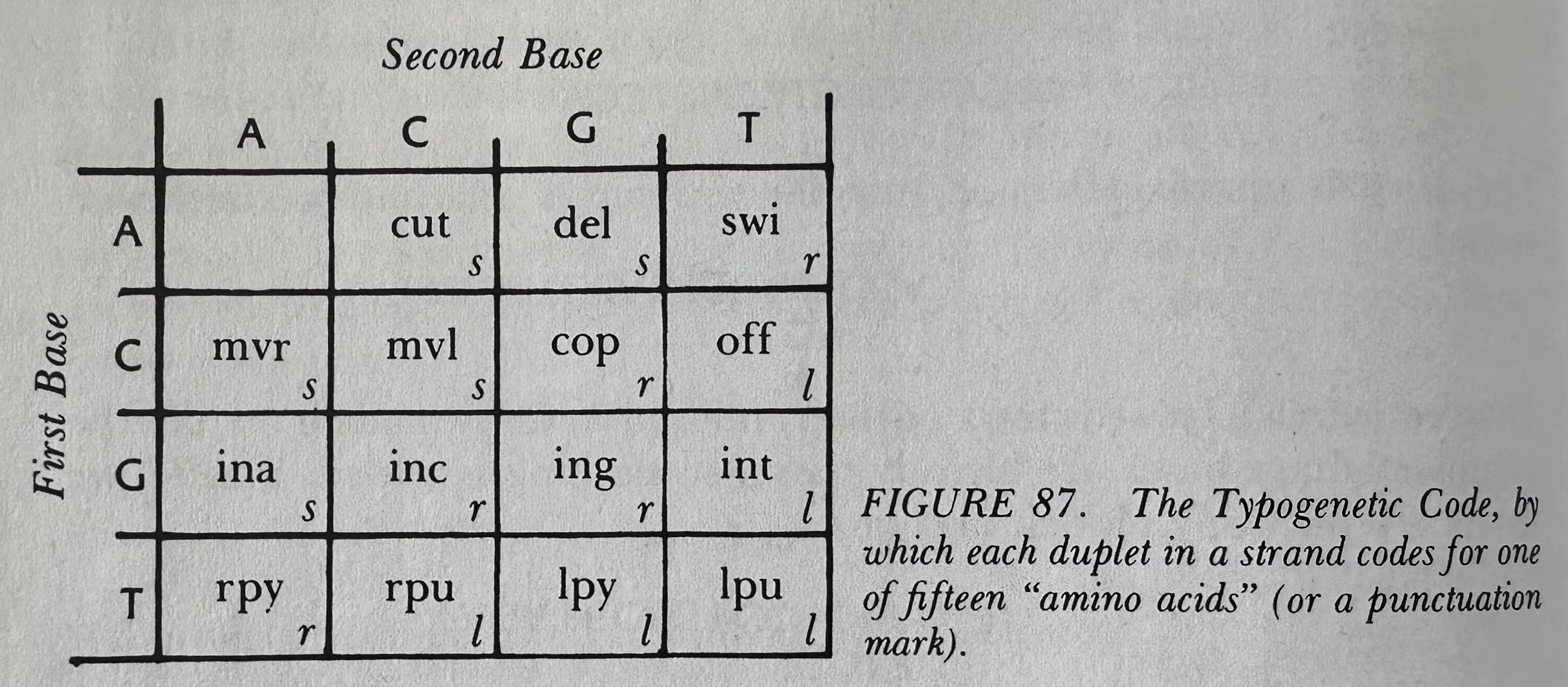
Complementary Base Pairing: Purines (A, G) pair with Pyrimidines (T, C) in strings to create amino acids.
Amino Acids & Enzymes: There are 20 Amino Acids in the human body. Every enzyme is made up of a sequence of amino acids. Thus, each strand can be translated into one or more enzymes. Thus, the strands themselves will dictate the operations which will be performed upon them, and those operations will in turn produce new strands which will dictate further enzymes. In order to figure out what letter an enzyme likes to bind to, you have to figure out the enzyme's "tertiary structure", which is itself determined by the enzyme's "primary structure". By its primary structure is meant its amino acid sequence. By its tertiary structure is meant the way it likes to "fold up". The relative orientation of the first and last segments of an enzyme's tertiary structure determines the binding-preference of the enzyme.
Enzymes: Make practically every life process go; are manufactured by ribosomes in the cytoplasm.
Here's a sample enzyme, consisting of three operations: (1) Delete the unit to which the enzyme is bound (and then bind to the next unit to the right). (2) Move one unit to the right. (3) Insert a T (to the immediate right of this unit). This enzyme happens to like to bind to A initially. And here's a sample strand: ACA. What happens if our enzyme binds to the left A and begins acting? Step 1 deletes the A, so we are left with CA- and the enzyme is now bound to the C. Step 2 slides the enzyme rightwards, to the A, and Step 3 appends a T onto the end to form the strand CAT. And the enzyme has done its complete duty: it has transformed ACA into CAT.
Gene: The portion of a DNA strand which codes for a single enzyme.
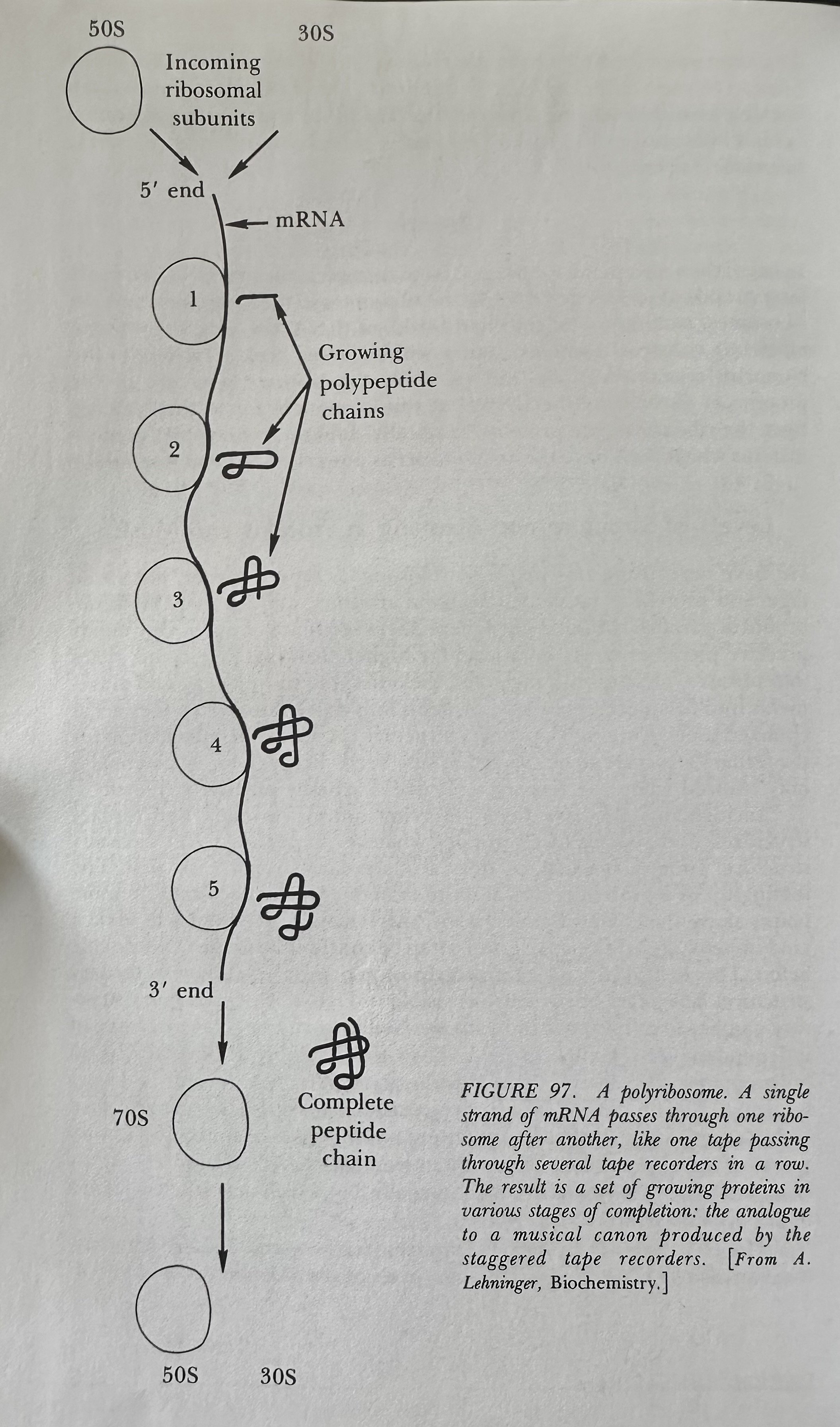
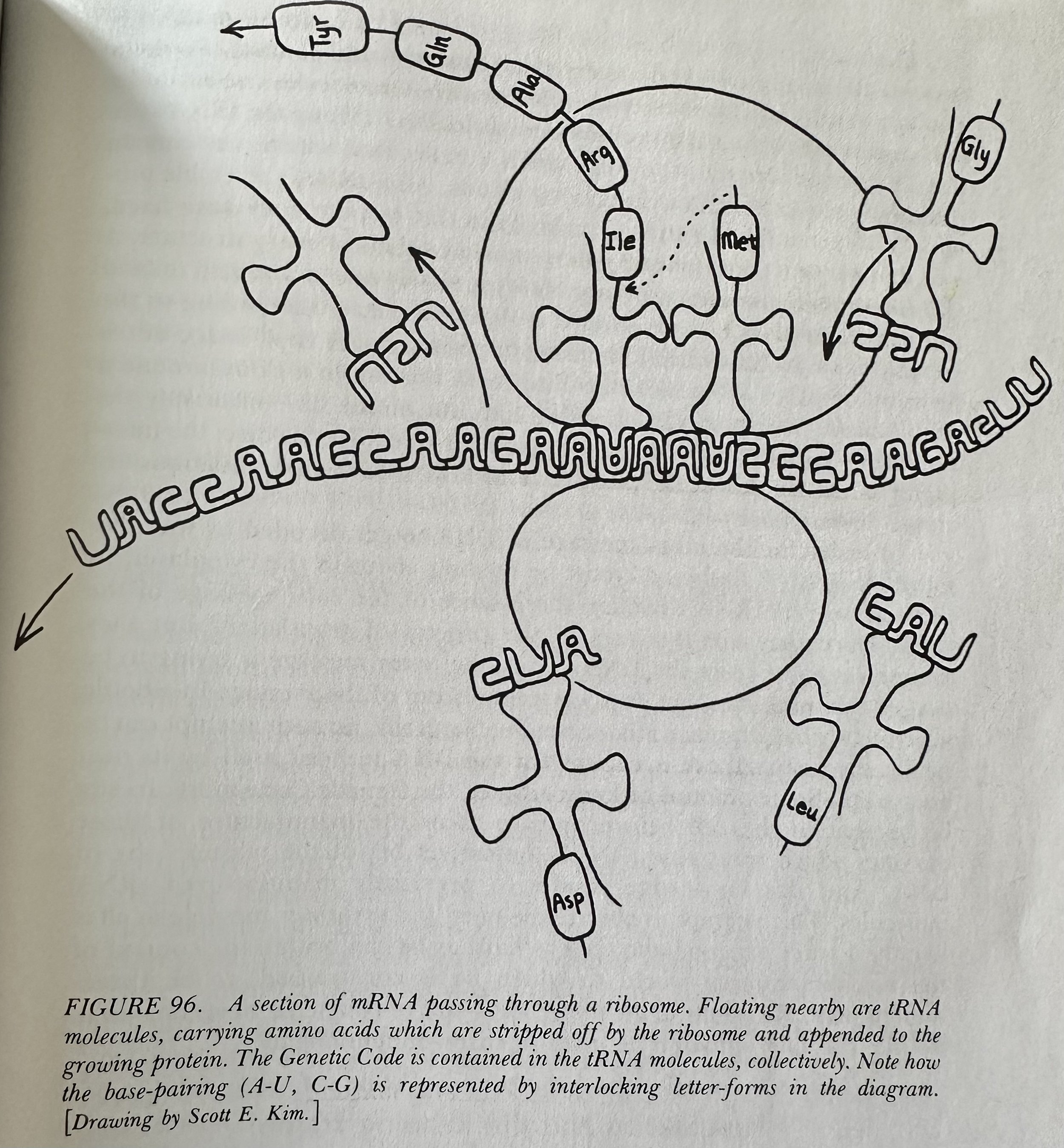
Ribosome: The mechanism which reads strands and produces the enzymes which are coded inside them. The process of translation always goes from strands to enzymes.
Strands are acted upon, and therefore play the role of data; on the other hand, they also dictate the actions which are to be performed on the data, and therefore they play the role of programs.
Deoxyribonucleic Acid (DNA): The DNA of most cells resides in the cell's nucleus, which is a small area protected by a membrane. DNA consists of long chains of relatively simple molecules called nucleotides. Each nucleotide is made up of three parts: 1) a phosphate group stripped of one special O atom, whence the prefix "deoxy"; 2) a sugar called "ribose" , and 3) a base. The four types of bases which occur in DNA nucleotides are A, G, C, T.
The chemical bond which links a nucleotide to its two neighbors is very strong; such bonds are called covalent bonds, and the "chain of beads" is often called the covalent backbone of DNA. Compared to the strong covalent bonds along the backbone, the inter-strand bonds are quite weak. They are not covalent bonds, but H bonds. A H bond arises when two molecular complexes are aligned in such a way that a H atom which originally belonged to one of them becomes "confused" about which one it belongs to, and it hovers between the two complexes, vacillating as to which one to join.
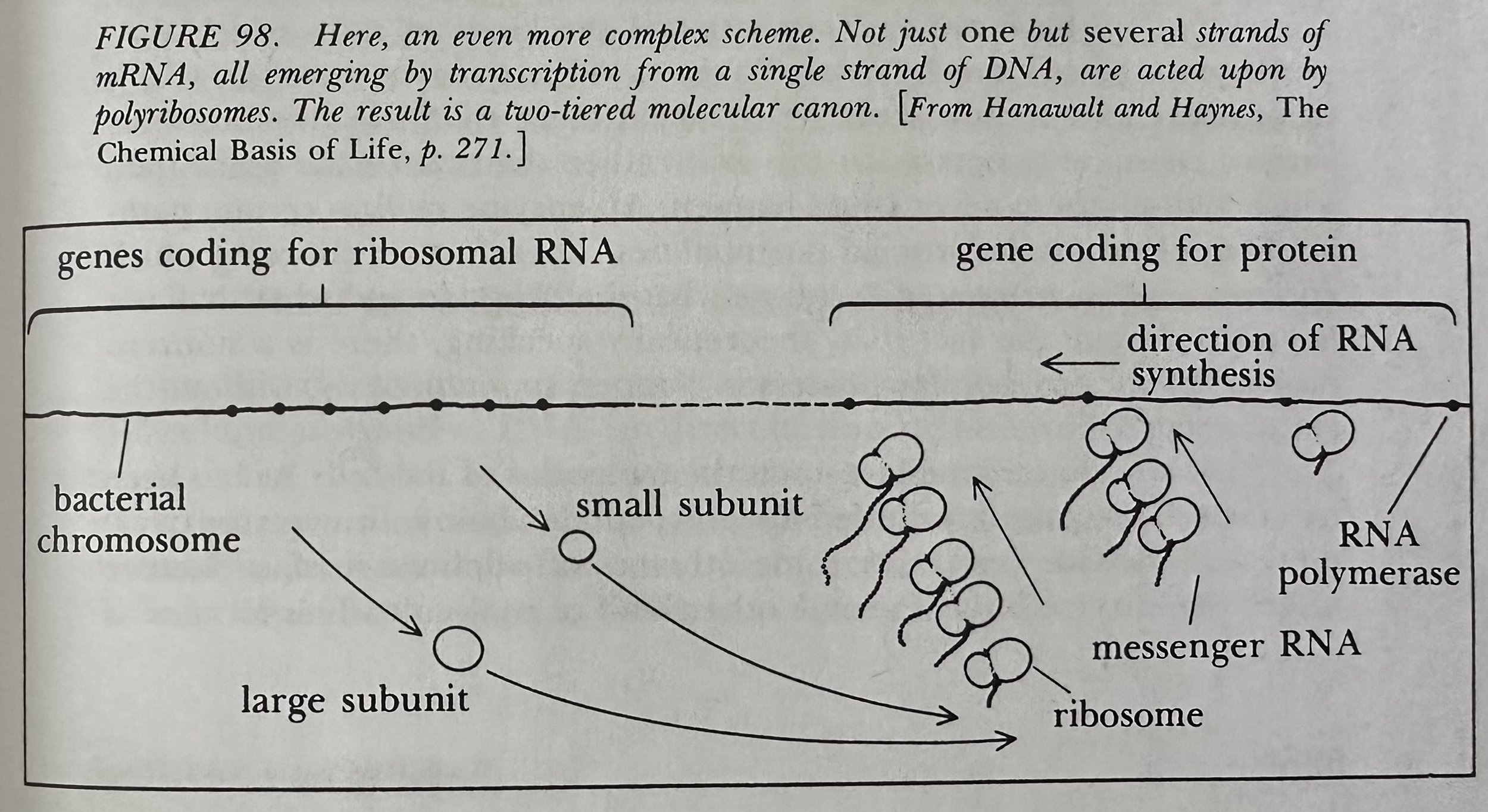
Messenger RNA (mRNA): Carries the information, or message, stored in the DNA out to the ribosomes in the cytoplasm via an enzyme inside the nucleus that copies long stretches of the DNA's base sequence onto a new strand- a strand of messenger RNA. This mRNA then departs from the nucleus and wanders out into the cytoplasm, where it runs into many ribosomes which begin doing their enzyme- creating work on it.
Transcription: The process by which DNA gets copied onto mRNA inside the nucleus.
In the nucleus of the cell the double-stranded DNA must be temporarily separated into two single strands, one of which serves as a template for the mRNA. Now when mRNA is transcribed off of DNA, the transcription process operates via the usual base-pairing (except with U instead of T), so that a DNA-template and its mRNA-mate might look something like this:
DNA: CGTAAATCAAGTCA (template)
mRNA: GCAUUUAGUUCAGU (copy)
Ribonucleic Acid (RNA): Very much like DNA except that all of its nucleotides possess that special O atom in the phosphate group which DNA's nucleotides lack (therefore the "deoxy" prefix is dropped). Also, instead of thymine, RNA uses the base uracil, so the information in strands of RNA can be represented by arbitrary sequences of the four letters 'A', 'C, 'G', U.
Proteins: (Which are not enzymes) structural molecules- like girders and beams in buildings- they hold the cell's parts together. There are other kinds of proteins, but for our purposes, the principal proteins are enzymes. Proteins are composed of sequences of amino acids, of which there are 20, each with a three-letter abbreviation:
Alanine (Ala); Arginine (Arg); Asparagine (Asn); Aspartic Acid (Asp); Cysteine (Cys); Glutamine (Gln); Glycine (Gly); Histidine (His); Isoleucine (Ile); Leucine (Leu); Lysine (Lys); Methionine (Met); Phenylalanine (Phe); Proline (Pro); Serine (Ser); Threonine (Thr); Tryptophan (Trp); Tyrosine (Tyr); Valine (Val).
Proteins are composed of much shorter sequences of components: typically, ~300 amino acids make a complete protein, whereas a strand of DNA can consist of hundreds of thousands or millions of nucleotides.
As a protein emerges from a ribosome, it is not only getting longer and longer, but it is also continually folding itself up into an extraordinary 3D shape, very much in the way that those funny little Fourth-of-July fireworks called "snakes" simultaneously grow longer and curl up, when they are lit. This fancy shape is called the protein's tertiary structure, while the amino acid sequence per se is called the primary structure of the protein. The tertiary structure is implicit in the primary structure, just as in Typogenetics. However, the recipe for deriving the tertiary structure, if you know only the primary structure, is by far more complex than that given in Typogenetics (in fact, it is one of the outstanding problems of contemporary molecular biology to figure out some rules by which the tertiary structure of a protein can be predicted if only its primary structure is known)
In real enzymes, individual amino acids cannot be assigned such clear roles. It is the tertiary structure as a whole which determines the mode in which an enzyme will function.
The function of a protein cannot be considered to be built up from context- free functions of its parts; rather, one must consider how the parts interact.
There are, floating about in the cytoplasm at any given moment, large numbers of four-leaf-clover-shaped molecules; loosely fastened (i.e., H-bonded) to one leaf is an amino acid, and on the opposite leaf there is a triplet of nucleotides called an anticodon. For our purposes, the other two leaves are irrelevant. Here is how these "clovers" are used by the ribosomes in their production of proteins. When a new codon of mRNA clicks into position in the ribosome's "playing head", the ribosome reaches out into the cytoplasm and latches onto a clover whose anticodon is complementary to the mRNA codon. Then it pulls the clover into such a position that it can rip off the clover's amino acid, and stick it covalently onto the growing protein. (Incidentally, the bond between an amino acid and its neighbor in a protein is a very strong covalent bond, called a "peptide bond". For this reason, proteins are sometimes called "polypeptides".) Of course, it is no accident that the "clovers" carry the proper amino acids, for they have all been manufactured according to precise instructions emanating from the "throne room".
Transfer RNA (tRNA): Consists of a chain of ~80 nucleotides. Like mRNA, tRNA are made by transcription. tRNA have fixed, well-defined tertiary structures- determined by their primary structure. A tRNA molecules tertiary structure allows precisely one amino acid to bind to its amino-acid site.
The interpreter is the ribosome, the words are codons, and their translations are amino acids.
How does a ribosome know when a protein is done? Just as in Typogenetics, there is a signal inside the mRNA which indicates the termination or initiation of a protein. In fact, three special codons- UAA, UAG, UGA- act as punctuation marks instead of coding for amino acids. Whenever such a triplet clicks its way into the "reading head" of a ribosome, the ribosome releases the protein under construction and begins a new one.
In brief- from its central throne, DNA sends off long strands of mRNA to the ribosomes in the cytoplasm; and the ribosomes, making use of the "flashcards" of tRNA hovering about them, efficiently construct proteins, amino acid by amino acid, according to the blueprint contained in the mRNA. Only the primary structure of the proteins is dictated by the DNA; but this is enough, for as they emerge from the ribosomes, the proteins "magically" fold up into complex conformations which then have the ability to act as powerful chemical machines.
Ribosomes: Composed of various kinds of proteins and ribosomal RNA (rRNA; translate mRNA into proteins;
Enzymes: All enzymes are catalysts, which means they selectively accelerate various chemical processes in the cell.
How do enzymes act upon the molecules of the cell? Enzymes are folded-up polypeptide chains. In every enzyme, there is a cleft or pocket or some other clearly defined surface feature where the enzyme binds to some other kind of molecule.
Each enzyme's active site acts as a filter which only recognizes certain kinds of substrates (messages). Thus, an enzyme has an "address", in effect. The enzyme is "programmed" (by virtue of its tertiary structure) to carry out certain operations upon that "message", and then to release it to the world again.
T4 phage (virus): When a T4 phage invades an E. coli cell, after ~24-25 min, the cell has been subverted, and breaks open. Out pop ~200 exact copies of the original virus- "bi-centuplets"- ready to go attack more bacterial cells. The phage asserts its own producibility in a specific cell. Timing is as follows:
0 min: Injection of viral DNA.
1 min: Breakdown of host DNA. Cessation of production of native proteins and initiation of production of alien (T4) proteins. Among the earliest produced proteins are those which direct the replication of the alien (T4) DNA.
5 min: Replication of viral DNA begins.
8 min: Initiation of production of structural proteins which will form the “bodies” of new phages.
13 min: First complete replica of T4 invaders is produced.
25 min: Lysozyme (protein) attacks hose cell wall, breaking open the bacterium, and the “bicentuplets” emerge.
Enzyme Repression: Occurs via inhibition and/or repression.
Inhibition: Prevention of enzyme activity by “clogging-up” their active sites.
Repression: Prevention of enzyme activity by stopping the manufacture of certain enzymes.
It has been theorized that the difference between two neighboring cells which share the exact same genotype and yet have different functions is that different segments of their genome have been repressed, and therefore they have different working sets of proteins. A hypothesis like this could account for the phenomenal differences between cells in different organs of the body of a human being.
Since DNA contains all the information for construction of proteins, which are the active agents of the cell, DNA can be viewed as a program written in a higher-level language, which is subsequently translated (or interpreted) into the "machine language" of the cell (proteins). On the other hand, DNA is itself a passive molecule which undergoes manipulation at the hands of various kinds of enzymes; in this sense, a DNA molecule is exactly like a long piece of data, as well. Thirdly, DNA contains the templates off of which the tRNA "flashcards" are rubbed, which means that DNA also contains the definition of its own higher-level language. Proteins are active molecules, and carry out all the functions of the cell; therefore, it is quite appropriate to think of them as programs in the "machine language" of the cell (the cell itself being the processor). On the other hand, since proteins are hardware and most programs are software, perhaps it is better to think of the proteins as processors. Thirdly, proteins are often acted upon by other proteins, which means that proteins are often data. Finally, one can view proteins as interpreters; this involves viewing DNA as a collection of high-level language programs, in which case enzymes are merely carrying out the programs written in the DNA code, which is to say, the proteins are acting as interpreters. Then there are ribosomes and tRNA molecules. They mediate the translation from DNA to proteins, which can be compared to the translation of a program from a high-level language to a machine language; in other words, the ribosomes are functioning as interpreters and the tRNA molecules provide the definition of the higher-level language. But an alternative view of translation has it that the ribosomes are processors, while the tRNA's are interpreters.
___________________________________________________________________________
The Magnificrab, Indeed
Summary- The Magnificrab, Indeed: The title is a pun on Bach's Magnificat in D. The tale is about the Crab, who gives the appearance of having a magical power of distinguishing between true and false statements of number theory by reading them as musical pieces, playing them on his flute, and determining whether they are "beautiful" or not.
Crab: “Harrumph! I am not just an automatic music-machine, you know. Nor am I a garbage disposal for musical trash.”
___________________________________________________________________________
Ch. XVII: Church, Turing, Tarski, and Others
Summary- Chapter XVII: Church, Turing, Tarski, and Others. The fictional Crab of the preceding Dialogue is replaced by various real people with amazing mathematical abilities. The Church-Turing Thesis, which relates mental activity to computation, is presented in several versions of differing strengths. All are analyzed, particularly in terms of their implications for simulating human thought mechanically, or programming into a machine an ability to sense or create beauty. The connection between brain activity and computation brings up some other topics: the halting problem of Turing, and Tarski's Truth Theorem.
One of the main theses of this book is that every aspect of thinking can be viewed as a high-level description of a system which, on a low level, is governed by simple, even formal, rules. The "system" , of course, is a brain.
Hardy describes what he perceived as Ramanujan's outstanding intellectual attributes: With his memory, his patience, and his power of calculation, he combined a power of generalization, a feeling for form, and a capacity for rapid modification of his hypotheses, that were often really startling, and made him, in his own field, without a rival in his day.
Church’s Theorem: There is no infallible method for telling theorems of TNT from nontheorems.
Tarski-Church-Turing Theorem: There is no infallible method for telling true from false statements of number theory.
Church-Turing Thesis, Tautological Version: Mathematics problems can be solved only by doing mathematics.
Church-Turing Thesis, Reductionists Version: All brain processes are derived from a computable substrate.
Church-Turing Thesis, Theodore Roszak Version: Computers are ridiculous. So is science in general.
AI Thesis: As the intelligence of machines evolves, its underlying mechanisms will gradually converge to the mechanisms underlying human intelligence.
Historically, people have been naïve about what qualities, if mechanized, would undeniably constitute intelligence. Sometimes it seems as though each new step towards Al, rather than producing something which everyone agrees is real intelligence, merely reveals what real intelligence is not. If intelligence involves learning, creativity, emotional responses, a sense of beauty, a sense of self, then there is a long road ahead, and it may be that these will only be realized when we have totally duplicated a living brain.
Another way of characterizing the difference between "syntactic" and "semantic" properties is that the syntactic ones reside inside the object under consideration, whereas semantic properties depend on its relations with a potentially infinite class of other objects, and therefore are not completely localizable. There is nothing cryptic or hidden, in principle, in syntactic properties, whereas hiddenness is of the essence in semantic properties. That is the reason for my suggested distinction between "syntactic" and "semantic" aspects of visual form.
___________________________________________________________________________
SHRDLU, Toys of Man’s Designing
Summary- SHRDLU, Toy of Man's Designing: This Dialogue is lifted out of an article by Terry Winograd on his program SHRDLU; only a few names have been changed. In it, a program communicates with a person about the so-called "blocks world" in rather impressive English. The computer program appears to exhibit some real understanding-in its limited world. The Dialogue's title is based on Jesu, Joy of Man's Desiring, one movement of Bach's Cantata 147.
___________________________________________________________________________
Ch. XVIII: Artificial Intelligence: Retrospects
Summary- Chapter XVIII: Artificial Intelligence: Retrospects: This Chapter opens with a discussion of the famous "Turing test"- a proposal by Alan Turing for a way to detect the presence or absence of "thought" in a machine. From there, we go on to an abridged history of Artificial Intelligence. This covers programs that can- to some degree- play games, prove theorems, solve problems, compose music, do mathematics, and use natural language(e.g., English).
Champernowne and Turing were both avid chess players and invented "round-the-house" chess: after your move, run around the house if you get back before your opponent has moved, you're entitled to another move
Turing Test (Imitation Game): “It is played with three people: a man A), a woman B), and an interrogator C) who may be of either sex. The interrogator stays in a room apart from the other two. The object of the game for the interrogator is to determine which of the other two is the man and which is the woman. He knows them by labels X and Y, and at the end of the game he says either “X is A and Y is B” or “X is B and Y is A.” The interrogator is allowed to put questions to A and B thus: C: Will X please tell me the length of his or her hair? Now suppose X is actually A, then A must answer. It is A's object in the game to try to cause C to make the wrong identification. His answer might therefore "My hair is shingled, and the longest strands are about nine inches long." In order that that tones of voice may not help the interrogator the answers should be written, or better still, typewritten. The ideal arrangement is to have a teleprinter communicating between the two rooms. Alternatively, the questions and answers can be repeated by an intermediary. The object of the game for the third player (B) is to help the interrogator. The best strategy for her is probably to give truthful answers. She can add such things as I am the woman, don't listen to him!" to her answers, but it will avail nothing as the man can make similar remarks.”
Turing anticipates nine objections:
Theological Objection: Thinking is a function of man's immortal soul. God has given an immortal soul to every man and woman, but not to any other animal or to machines. Hence no animal or machine can think.
"Heads in the Sand" Objection: The consequences of machines thinking would be too dreadful. Let us hope and believe that they cannot do so.
Mathematical Objection: (This is essentially the Lucas argument).
Argument from Consciousness: "Not until a machine can write a sonnet or compose a concerto because of thoughts and emotions felt, and not by the chance fall of symbols, could we agree that machine equals brain that is, not only write it but know that it had written it. No mechanism could feel (and not merely artificially signal, an easy contrivance) pleasure at its successes, grief when its valves fuse, be warmed by flattery, be made miserable by its mistakes, be charmed by sex, be angry or depressed when it cannot get what it wants” (Professor Jefferson).
Arguments from Various Disabilities: These arguments take the form, "I grant you that you can make machines do all the things that you have mentioned but you will never be able to make one to do X." Numerous features X are suggested in this connection. I offer a selection. Be kind, resourceful, beautiful, friendly, have initiative, have a sense of humor, tell right from wrong, make mistakes, fall in love, enjoy strawberries and cream, make someone fall in love with it, learn from experience, use words properly, be the subject of its own thought, have as much diversity of behaviour as a man, do something really new.
Lady Lovelace's Objection: Our most detailed information of Babbage's Analytical Engine comes from a memoir by Lady Lovelace. In it she states, "The Analytical Engine has no pretensions to originate anything. It can do whatever we know how to order it to perform.”
Argument from Continuity in the Nervous System: The nervous system is certainly not a discrete state machine. A small error in the information about the size of a nervous impulse impinging on a neuron may make a large difference to the size of the outgoing impulse. It may be argued that, this being so, one cannot expect to be able to mimic the behaviour of the nervous system with a discrete state system.
Argument from Informality of Behaviour: It seems to run something like this. "If each man had a definite set of rules of conduct by which he regulated his life he would be no better than a machine. But there are no such rules, so men cannot be machines."
Argument from Extra-Sensory Perception: Let us play the imitation game, using as witnesses a man who is good as a telepathic receiver, and a digital computer.
This is, it seems to me, a general principle: you get bored with something not when you have exhausted its repertoire of behavior, but when you have mapped out the limits of the space that contains its behavior.
The top twelve letters in English, in order, according to Mergenthaler, are: "ETAOIN SHRDLU"
___________________________________________________________________________
Contrafactus
Summary- Contrafactus: About how we unconsciously organize our thoughts so that we can imagine hypothetical variants on the real world all the time. Also, about aberrant variants of this ability-such as possessed by the new character, the Sloth, an avid lover of French fries, and rabid hater of counterfactuals.
___________________________________________________________________________
Ch. XIX: Artificial Intelligence: Prospects
Summary- Chapter XIX: Artificial Intelligence: Prospects: The preceding Dialogue triggers a discussion of how knowledge is represented in layers of contexts. This leads to the modern Al idea of "frames". A frame-like way of handling a set of visual pattern puzzles is presented, for the purpose of concreteness. Then the deep issue of the interaction of concepts in general is discussed, which leads into some speculations on creativity. The Chapter concludes with a set of personal "Questions and Speculations" on Al and minds in general.
Consider how natural it feels to slip from the valueless declarative "I don't know Russian" to the more charged conditional "I would like to know Russian" to the emotional subjunctive "I wish I knew Russian" and finally to the rich counterfactual "If I knew Russian, I would read Chekhov and Lermontov in the original". How flat and dead would be a mind that saw nothing in a negation but an opaque barrier! A live mind can see a window onto a world of possibilities I believe that "almost" situations and unconsciously manufactured subjunctives represent some of the richest potential sources of insight into how human beings organize and categorize their perceptions of the world.
frame + actor = symbol
Repetition has a way of burning new circuits into our mental hardware, so that oft-repeated pieces of behavior become encoded below the conscious level.
Concepts: Composed of tight and loose elements, coming from different levels of nested contexts (frames).
When programs cease to be transparent to their creators, then the approach to creativity has begun.
Perhaps what differentiates highly creative ideas from ordinary ones is some combined sense of beauty, simplicity, and harmony. In fact, I have a favorite "meta-analogy", in which I liken analogies to chords. The idea is simple: superficially similar ideas are often not deeply related; and deeply related ideas are often superficially disparate.
The elusive sense for patterns which we humans inherit from our genes involves all the mechanisms of representation of knowledge, including nested contexts, conceptual skeletons and conceptual mapping, slippability, descriptions and meta-descriptions and their interactions, fission and fusion of symbols, multiple representations along different dimensions and different levels of abstraction), default expectations, and more.
The amazing thing about language is how imprecisely we use it and still manage to get away with it.
Page 676-680: Ten Questions and Speculations on AI.
___________________________________________________________________________
Sloth Canon
Summary- Sloth Canon: A canon which imitates a Bach canon in which one voice plays the same melody as another, only upside down and twice as slowly, while a third voice is free. Here, the Sloth utters the same lines as the Tortoise does, only negated (in a liberal sense of the term) and twice as slowly, while Achilles is free.
___________________________________________________________________________
Ch. XX: Strange Loops, Or Tangle Hierarchies
Summary- Chapter XX: Strange Loops, Or Tangled Hierarchies: A grand windup of many of the ideas about hierarchical systems and self-reference. It is concerned with the snarls which arise when systems turn back on themselves-for example, science probing science, government investigating governmental wrongdoing, art violating the rules of art, and finally, humans thinking about their own brains and minds. Does Gödel's Theorem have anything to say about this last "snarl"? Are free will and the sensation of consciousness connected to Gödel's Theorem? The Chapter ends by tying Gödel, Escher, and Bach together once again.
Software rules on various levels can change; hardware rules cannot- in fact, to their rigidity is due the software's flexibility!
This distinction between self-modifiable software and inviolate hardware is what I wish to pursue in this final Chapter, developing it into a set of variations on a theme.
We humans operate without need of rules: we are "informal systems". On the other hand, as an argument against the possibility of any mechanical instantiation of reasoning, it is valid, for any mechanical reasoning-system would have to depend on rules explicitly, and so it couldn't get off the ground unless it had metarules telling it when to apply its rules, meta-metarules telling it when to apply its metarules, and so on. We may conclude that the ability to reason can never be mechanized. It is a uniquely human capability.
A central issue of this book is: "Do words and thoughts follow formal rules?" One major thrust of the book has been to point out the many- leveledness of the mind/brain, and I have tried to show why the ultimate answer to the question is, "Yes—provided that you go down to the lowest level- the hardware- to find the rules."
The point of this book has been to show, how in any system there is always some "protected" level which is unassailable by the rules on other levels, no matter how tangled their interaction may be among themselves.
Anarchy has its own kinds of rules, no less than does civilized society: it operates bottom up, not top down.
Is it possible to define what evidence is? Is it possible to lay down laws as to how to make sense out of situations? Probably not, for any rigid rules would undoubtedly have exceptions, and nonrigid rules are not rules.
My feeling is that the process by which we decide what is valid or what is true is an art; and that it relies as deeply on a sense of beauty and simplicity as it does on rock-solid principles of logic or reasoning or anything else which can be objectively formalized. I am not saying either 1) truth is a chimera, or 2) human intelligence is in principle not programmable. I am saying 1) truth is too elusive for any human or any collection of humans ever to attain fully; and 2) AI, when it reaches the level of human intelligence- or even if it surpasses it- will still be plagued by the problems of art, beauty, and simplicity, and will run up against these things constantly in its own search for knowledge and under-standing.
Gödel's Incompleteness Theorem, Church's Undecidability Theorem, Turing's Halting Theorem, Tarski's Truth Theorem- all have the flavor of some ancient fairy tale which warns you that "To seek self-knowledge is to embark on a journey which ... will always be incomplete, cannot be charted on any map, will never halt, cannot be described." But do the limitative Theorems have any bearing on people? Here is one way of arguing the case. Either I am consistent or I am inconsistent. (The latter is much more likely, but for completeness' sake, I consider both possibilities.) If I am consistent, then there are two cases. (1) The "low-fidelity case: my self-understanding is below a certain critical point. In this case, I am incomplete by hypothesis. (2) The "high-fidelity" case: My self-understanding has reached the critical point where a metaphorical analogue of the limitative Theorem does apply, so my self-understanding undermines itself in a Gödelian way, and I am incomplete for that reason. Cases (1) and (2) are predicated on my being 100% consistent—a very unlikely state of affairs. More likely is that I am inconsistent- but that's worse, for then inside me there are contradictions, and how can I ever understand that?
Tension and confusion are important in a world where many decisions must be made quickly. Miguel de Unamuno once said, "If a person never contradicts himself, it must be that he says nothing." I would say that we all are in the same boat as the Zen master who, after contradicting himself several times in a row, said to the confused Doko, "I cannot understand myself."
“All things in all of time and space are inextricably connected with one another. Any divisions, classifications, or organizations discovered in the universe are arbitrary. The world is a complex, continuous, single event.”-Meyer’s on Transcendentalism.
My belief is that the explanations of "emergent" phenomena in our brains- for instance, ideas, hopes, images, analogies, and finally consciousness and free will- are based on a kind of Strange Loop, an interaction between levels in which the top level reaches back down towards the bottom level and influences it, while at the same time being itself determined by the bottom level. In other words, a self-reinforcing "resonance" between different levels-quite like the Henkin sentence which, by merely asserting its own provability, actually becomes provable. The self comes into being at the moment it has the power to reflect itself.
Is there any reason to suspect that you would be able to change any of your own past decisions if every last detail- and that includes your brain, of course- were reset to the way it was the first time around? But let us return to the question of whether "choice" is an applicable term here. If programs are just "fancy marbles rolling down fancy hills", do they make choices, or not? Of course, the answer must be a subjective one, but I would say that pretty much the same considerations apply here as to the marble. However, I would have to add that the appeal of using the word "choice", even if it is only a convenient and evocative shorthand, becomes quite strong. The fact that a chess program looks ahead down the various possible bifurcating paths, quite unlike a rolling marble, makes it seem much more like an animate being than a square-root-of-2 program. However, there is still no deep self-awareness here-and no sense of free will.
If you were trapped inside a marble rolling down a hill and were powerless to affect its path, yet could observe it with all your human intellect, would you feel that the marble's path involved choices? Of course not. Unless your mind is affecting the outcome, it makes no difference that the symbols are present.
Unlike a standard chess program, which does not monitor itself and consequently has no ideas about where its moves come from, this program does monitor itself and does have ideas about its ideas- but it cannot monitor its own processes in complete detail, and therefore has a sort of intuitive sense of its workings, without full understanding. From this balance between self-knowledge and self-ignorance comes the feeling of free will.
___________________________________________________________________________
Six-Part Ricercar
Summary- Six-Part Ricercar: This Dialogue is an exuberant game played with many of the ideas which have permeated the book. It is a reenactment of the story of the Musical Offering, which began the book; it is simultaneously a "translation" into words of the most complex piece in the Musical Offering: the Six-Part Ricercar. This duality imbues the Dialogue with more levels of meaning than any other in the book. Frederick the Great is replaced by the Crab, pianos by computers, and so on. Many surprises arise. The Dialogue's content concerns problems of mind, consciousness, free will, Artificial Intelligence, the Turing test, and so forth, which have been introduced earlier. It concludes with an implicit reference to the beginning of the book, thus making the book into one big self-referential loop, symbolizing at once Bach's music, Escher's drawings, and Gödel's Theorem.
___________________________________________________________________________
Chronology
1946: Oswald Avery’s experiments show that, of all the biological molecules, only DNA transmits hereditary properties (GEB by Hofstadter).
1823: Hungarian mathematician János Bolyai, aged 21, and Russian mathematician Nikolay Lobachevsky, aged 30, discover non-Euclidean geometry (GEB by Hofstadter).
1740: Frederick the Great assumes power as King of Prussia (GEB by Hofstadter).
1202: Leonardo of Pisa, son of Bonaccio, ergo “Filius Bonacci”, discovers the Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13… (GEB by Hofstadter).
11c: Zen Buddhism arrives in Japan (GEB by Hofstadter).
6c: A monk named Bodhidharma leaves India for China and founds Zen Buddhism. In Zen, one seeks enlightenment, or ‘satori’, the state of “no-mind.” In this state, one does not think about the world, one just IS (GEB by Hofstadter).
300 BCE: Euclid’s pens “Elements” as a compilation of all of what was then known about plane and solid geometry (GEB by Hofstadter).
___________________________________________________________________________